Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

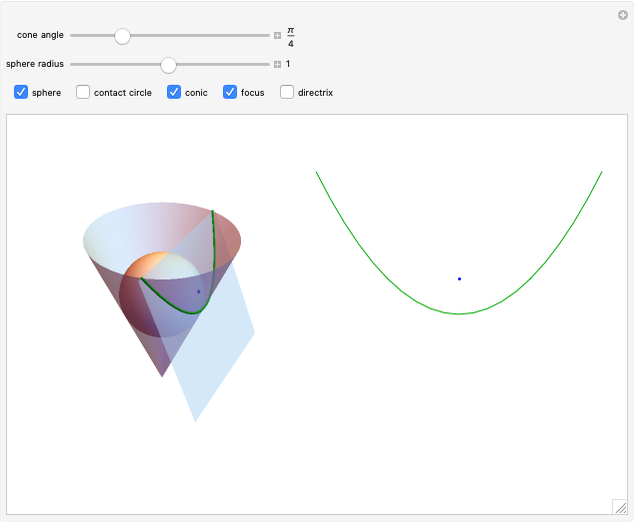
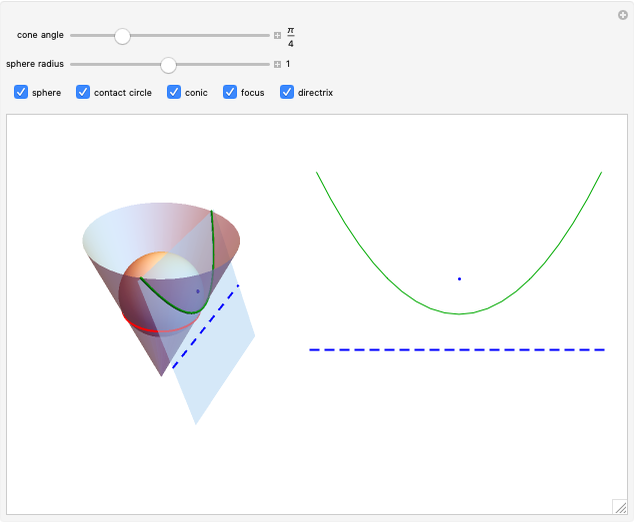
Dandelin Sphere for the Parabola

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

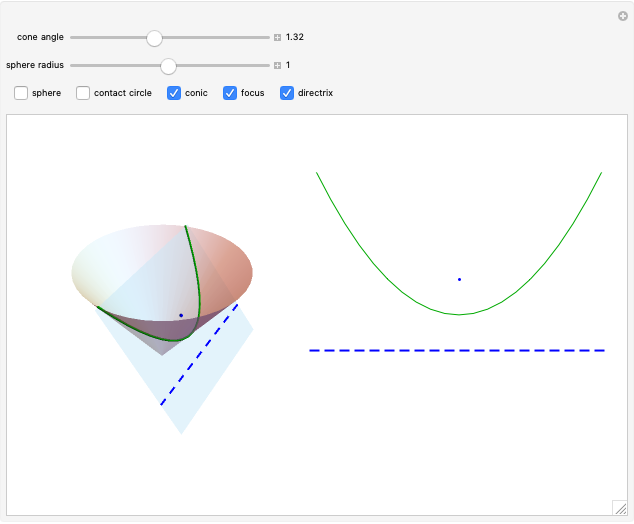
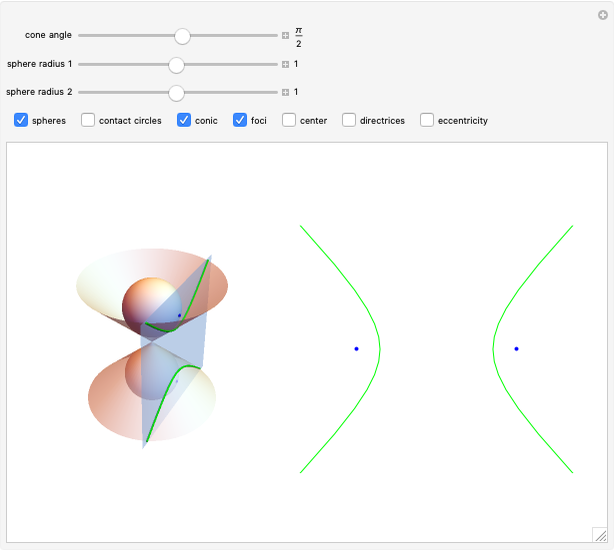
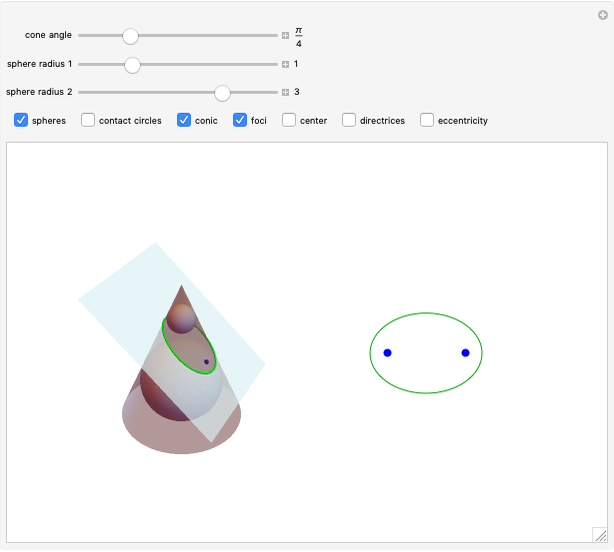
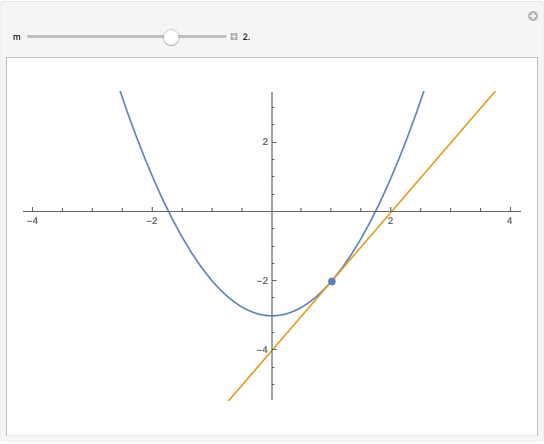
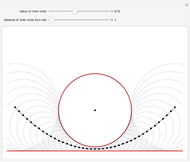
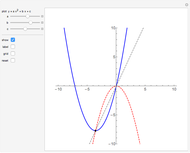
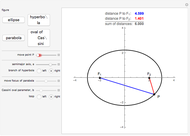
The parabola can be defined as the curve formed by the intersection of a cone with a plane parallel to a line on the cone passing through the origin. In this Demonstration, a Dandelin sphere shows the relationship between a parabola and its focus and directrix.

[more]

Dandelin's spheres have a special relationship with their associated conic section: their tangency points with the plane cutting the cone correspond to the foci of the conic section, while the planes through their circles of contact with the cone intersect the cutting plane in the conic section's directrices.

To get a very responsive Demonstration, the parabola and the contact circle are represented as nonuniform rational B-splines, avoiding the use of Wolfram Language plotting functions.

[less]

Contributed by: Jan Mangaldan (April 2020)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] L. Piegl and W. Tiller, The NURBS Book, 2nd ed., New York: Springer, 1997.

[2] C. Zwikker, The Advanced Geometry of Plane Curves and Their Applications, New York: Dover, 1963.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send