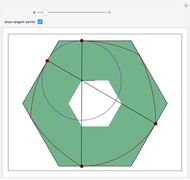
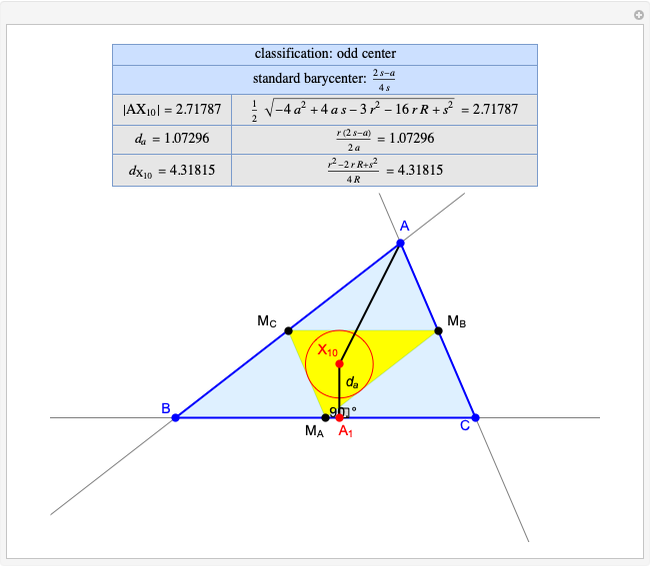
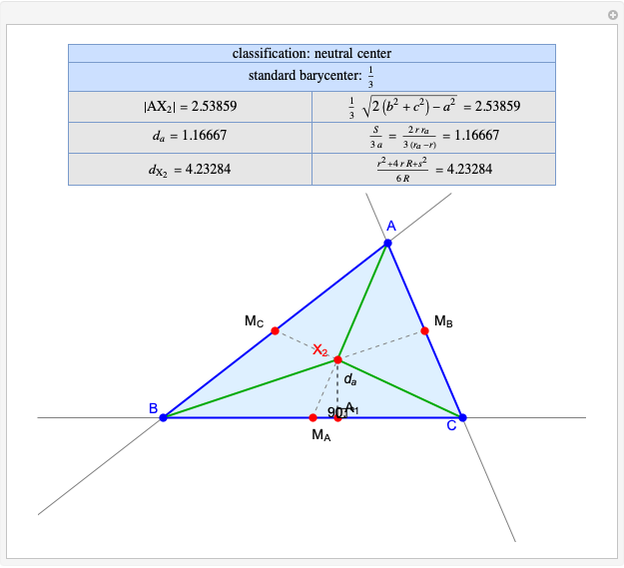
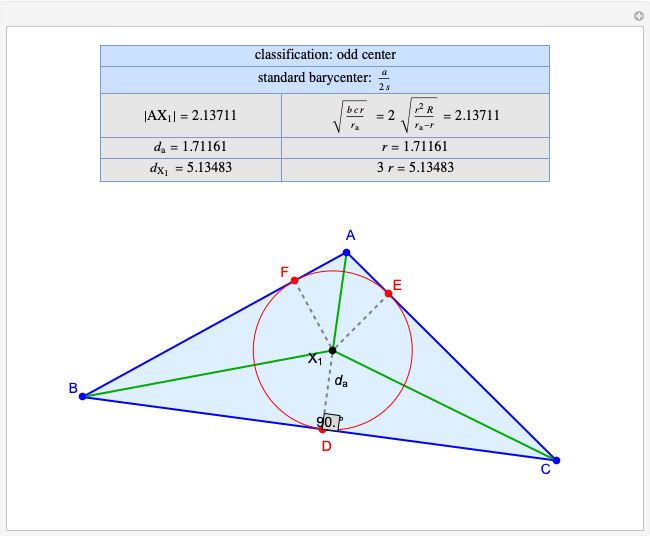
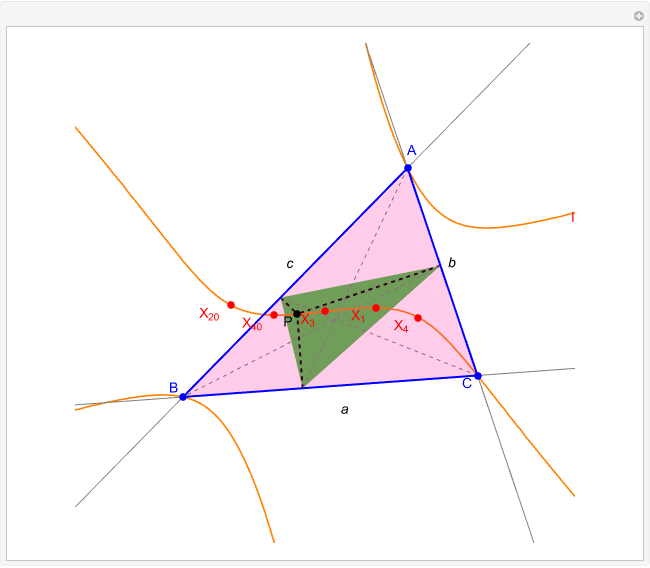
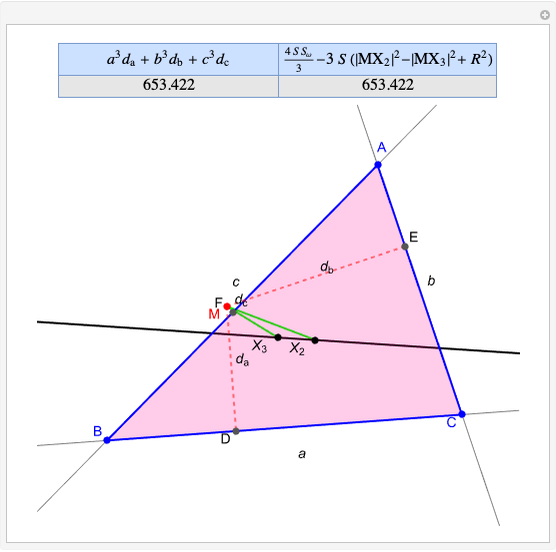
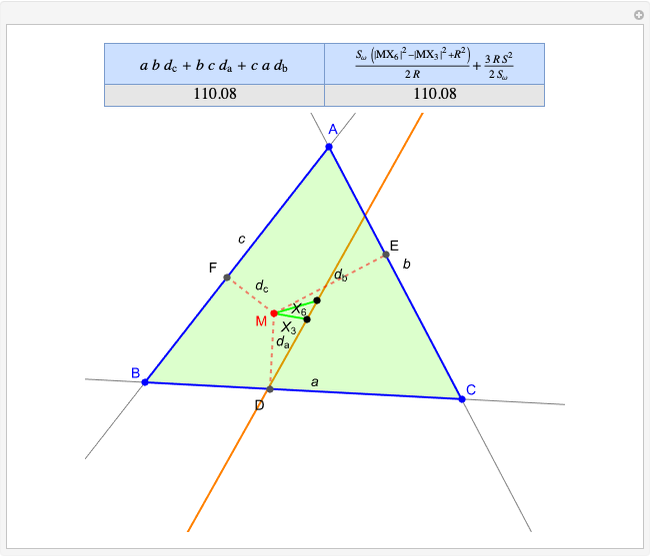
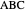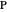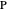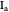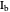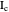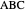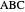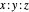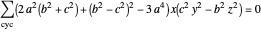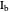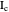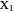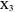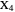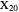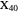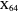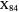Darboux Cubic
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
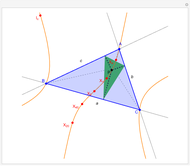
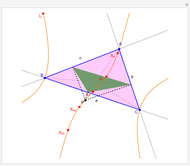
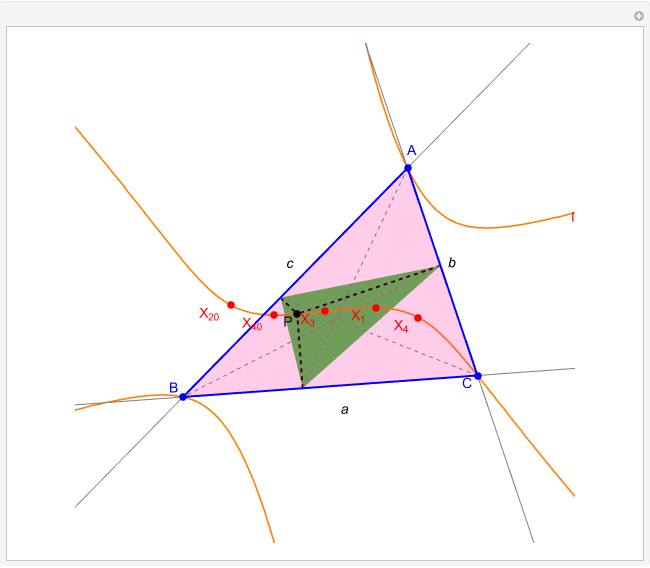
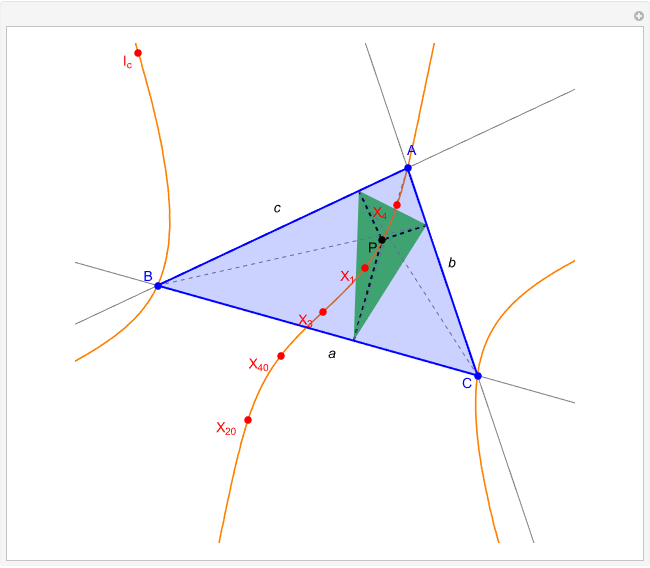
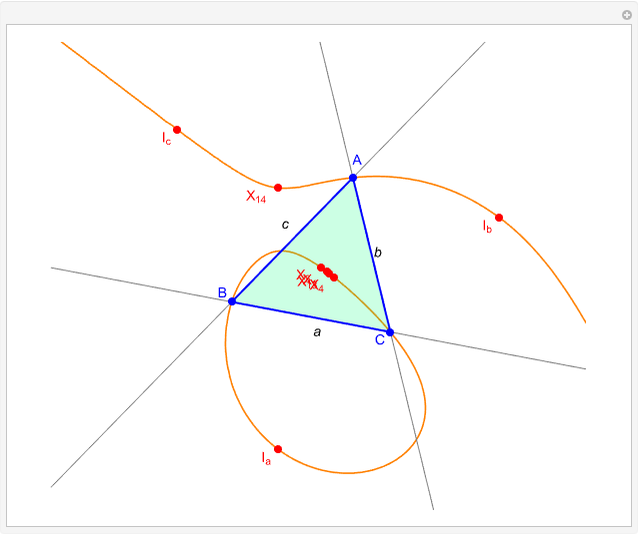
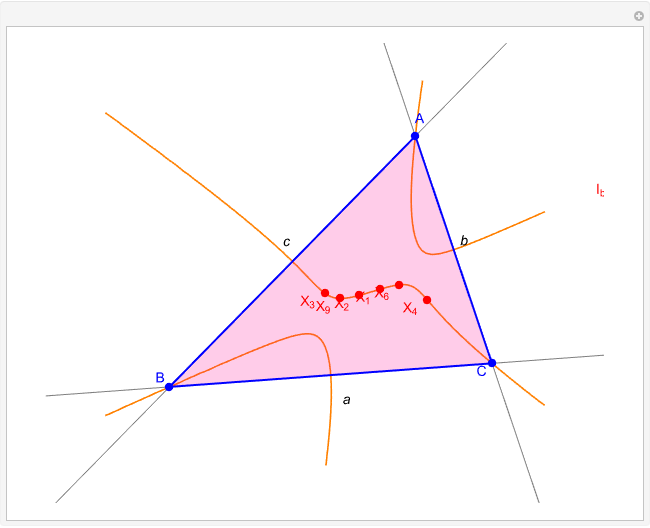
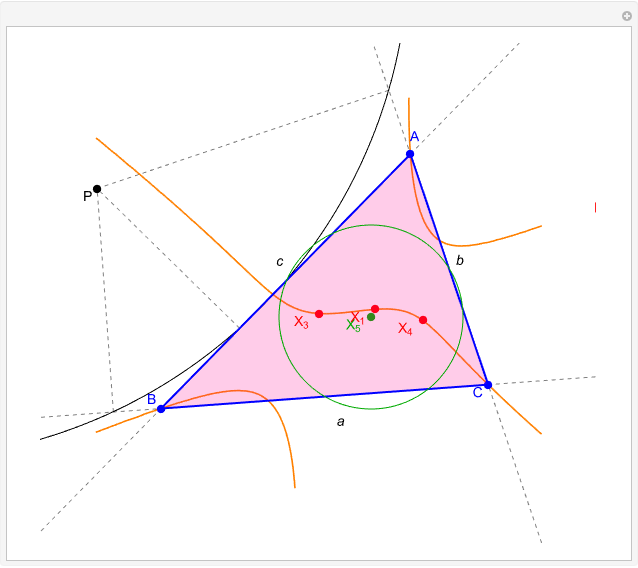
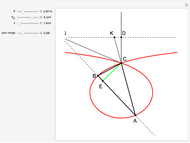
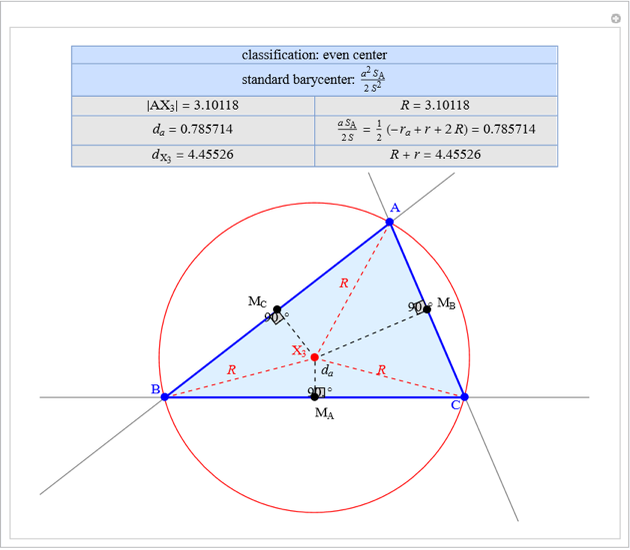
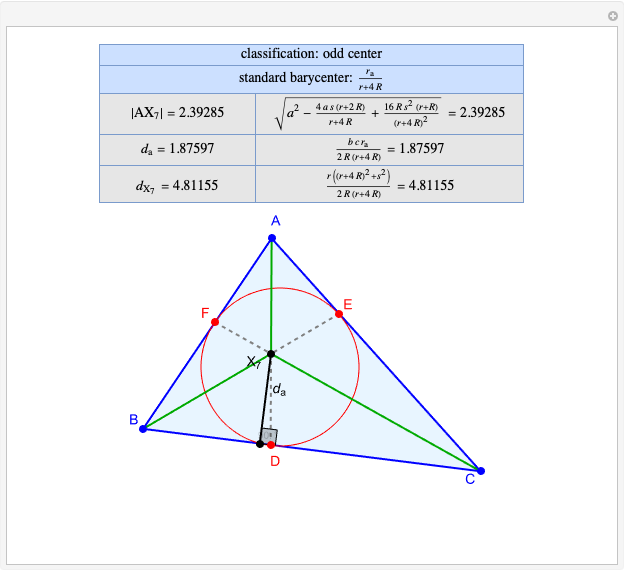
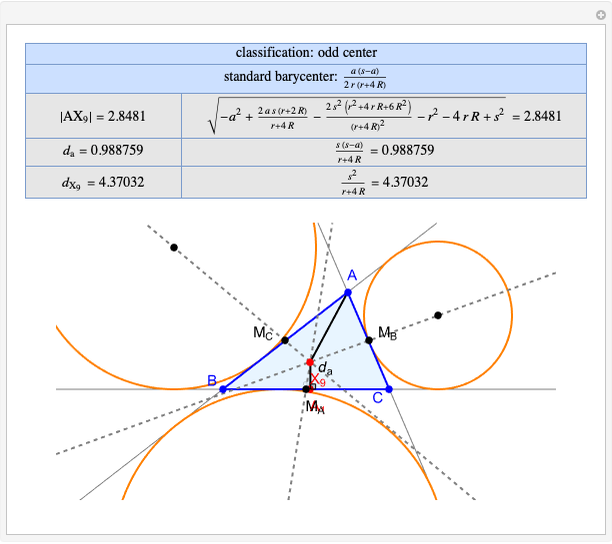
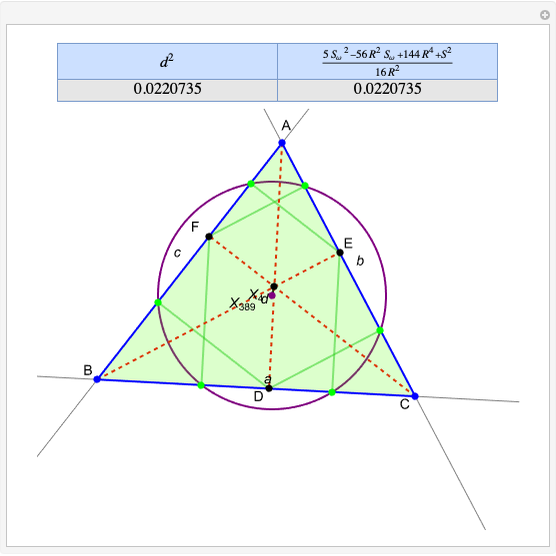
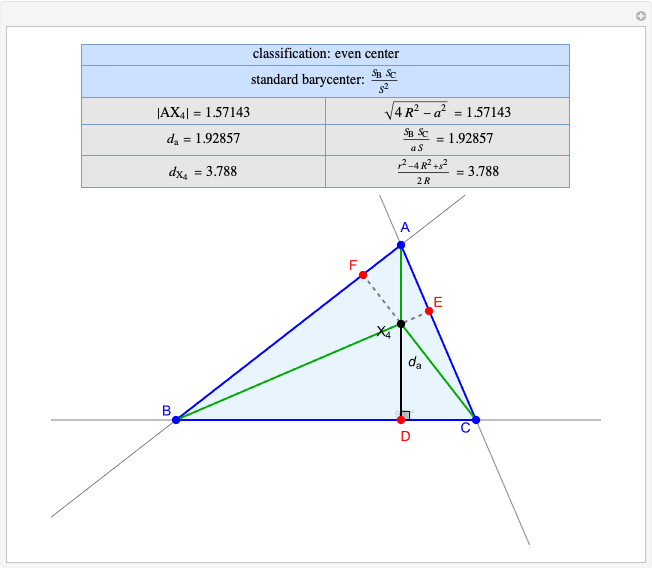
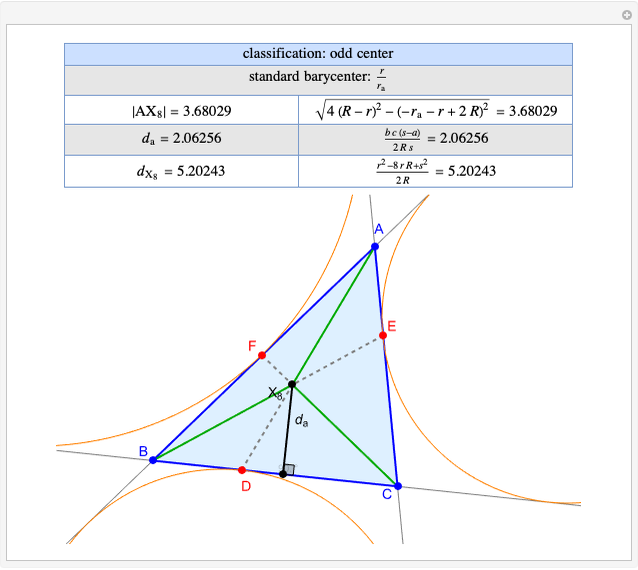
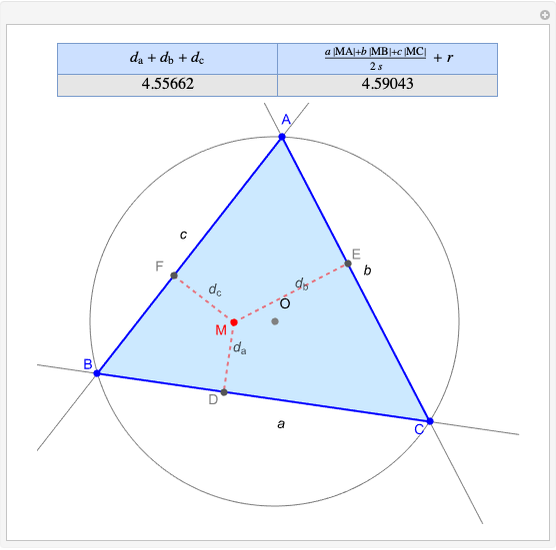
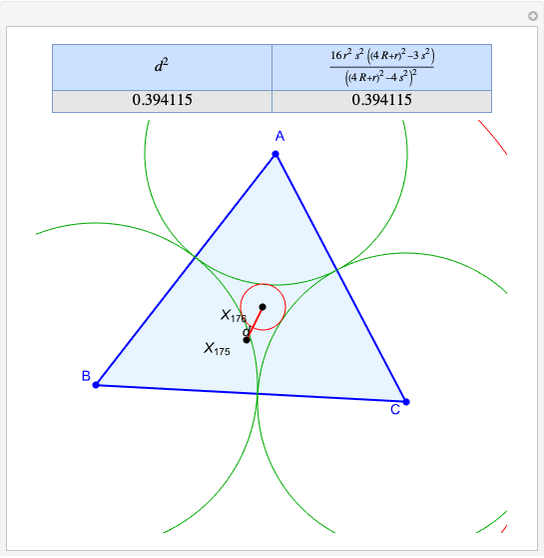
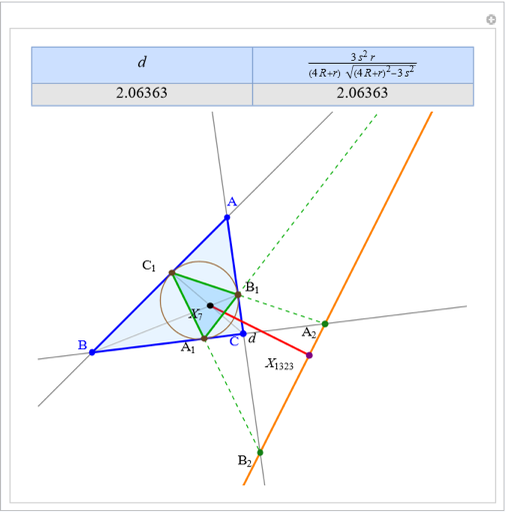
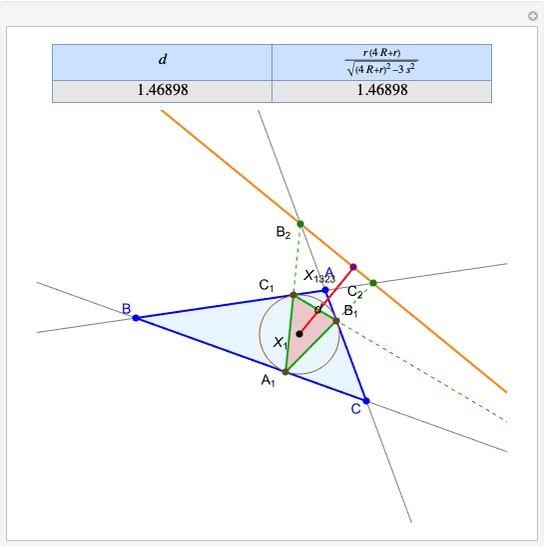
Given a triangle  and a point
and a point  , the pedal triangle of
, the pedal triangle of  is formed by the feet of the perpendiculars from
is formed by the feet of the perpendiculars from  to the three sides of triangle
to the three sides of triangle 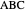 .
.
Contributed by: Minh Trinh Xuan (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] C. Kimberling, "Encyclopedia of Triangle Centers." http://faculty.evansville.edu/ck6/encyclopedia.
[2] B. Gilbert. "K004 Darboux Cubic = pk (X6, X20)." (Aug 2, 2022) bernard-gibert.pagesperso-orange.fr/Exemples/k004.html.
Permanent Citation