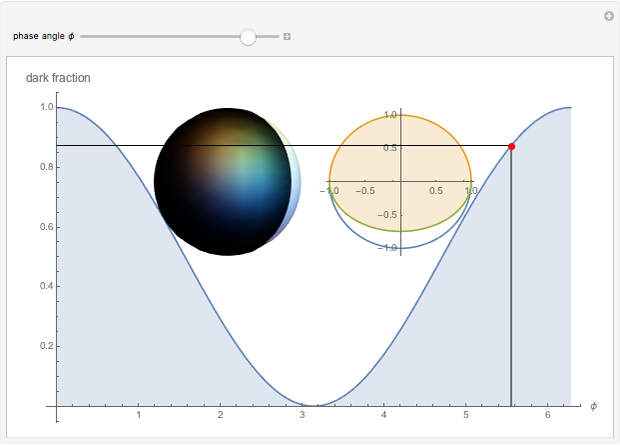
Dark Fraction of the Moon

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
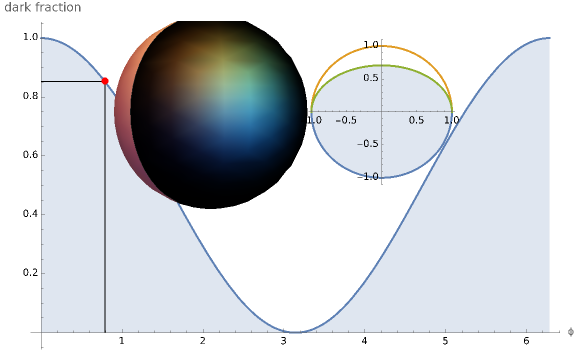
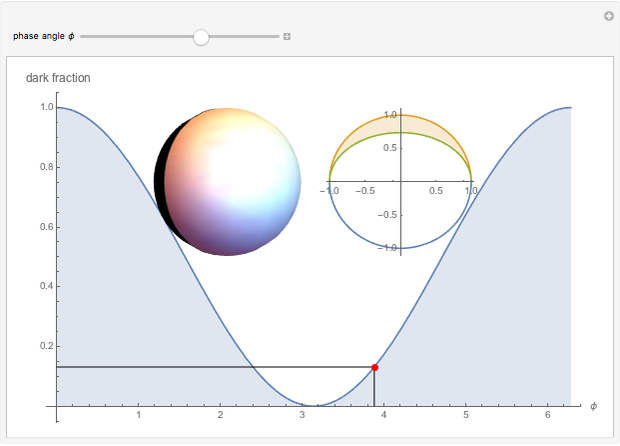
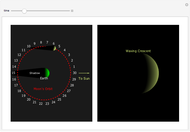
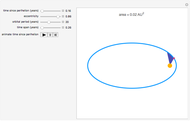
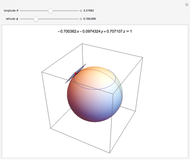
The fraction of the Moon that is dark is a function of the phase angle  . This function is
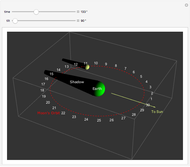
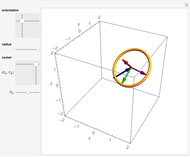
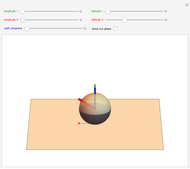
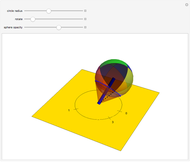
. This function is 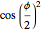 and can be found by taking an area integral over the circle. A sphere with one hemisphere black, the other hemisphere white, and rotated by
and can be found by taking an area integral over the circle. A sphere with one hemisphere black, the other hemisphere white, and rotated by  is shown in the top-left corner. The area integral being performed is shown in the top-right corner.
is shown in the top-left corner. The area integral being performed is shown in the top-right corner.
Contributed by: Aaron Becker (March 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For a unit radius sphere, the dividing equatorial line between the light and dark hemispheres projects to 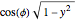 when
when  , and to
, and to 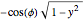 for
for 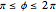 . Therefore when
. Therefore when 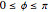 , the dark area is given by the area integral from the bottom of the sphere,
, the dark area is given by the area integral from the bottom of the sphere, 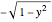 , to the dividing line
, to the dividing line 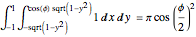 . Similarly, when
. Similarly, when 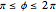 the dark area is given by the area integral from the dividing line to the top of the sphere,
the dark area is given by the area integral from the dividing line to the top of the sphere, 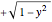 , and is
, and is 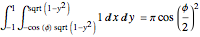 . Because the total area of the sphere is
. Because the total area of the sphere is  , dividing these area integrals by
, dividing these area integrals by  gives us the fraction that is dark,
gives us the fraction that is dark, 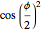 . The fraction of the moon that is illuminated is (1 – the fraction that is dark), and is given by
. The fraction of the moon that is illuminated is (1 – the fraction that is dark), and is given by 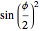 .
.
This quantity is derived in a different way in the following reference. Note that by the double-angle formula,  .
.
Reference
[1] D. B. Taylor, S. A. Bell, J. L. Hilton, and A. T. Sinclair, Computation of the Quantities Describing the Lunar Librations in the Astronomical Almanac, Ft. Belvoir: Defense Technical Information Center, 2010.
Permanent Citation