Desynchronization Dynamics of Two Coupled Oscillators

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
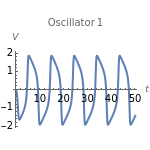
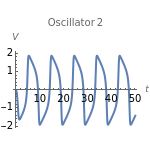
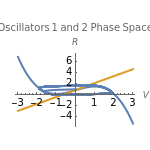
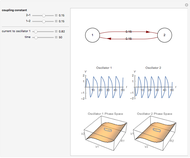
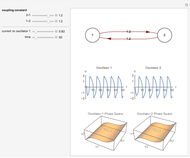
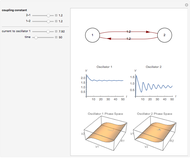
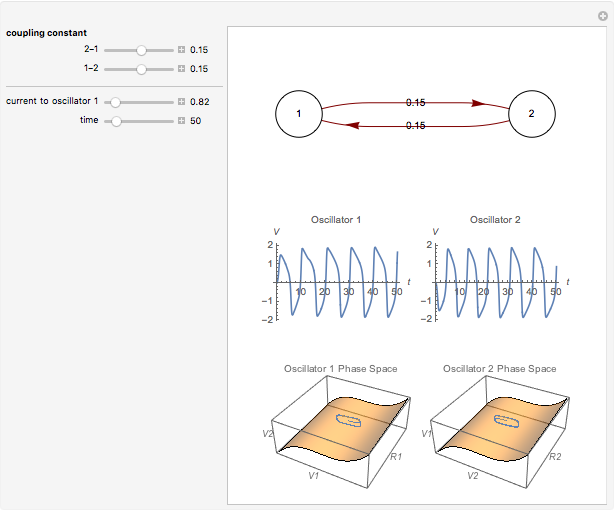
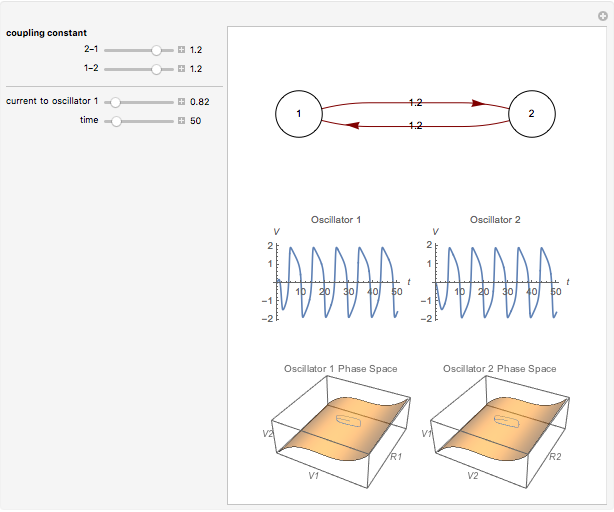
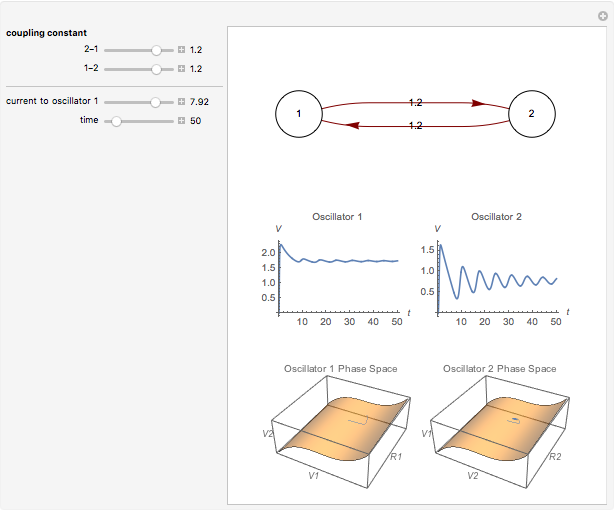
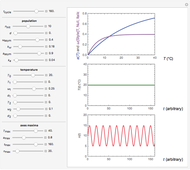
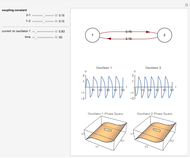
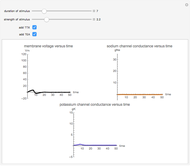
Neurons and neuronal networks can be modeled at many different levels, depending upon the phenomena one is modeling and the accuracy desired. In this Demonstration, neurons are considered as nonlinear phase oscillators that fire action potentials in accordance with the FitzHugh–Nagumo equations, two differential equations that are a simplification of the more biophysically involved Hodgkin–Huxley equations. Two neurons are initially synchronized trivially by being uncoupled. Interesting dynamical behavior can be observed when the neurons are coupled, both by excitation and inhibition. This behavior can be observed on a voltage-time axis for each neuron as well as in a state space, in which the trajectory about the equilibrium point is shown in either two or three dimensions.
Contributed by: Garrett Neske (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
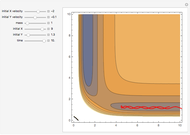
The two neurons are initially uncoupled and synchronized. When uncoupled, each neuron is a two-dimensional system described by a voltage ( ) and a recovery variable (
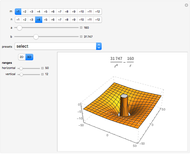
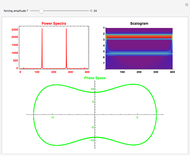
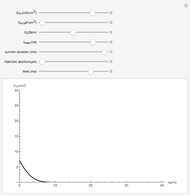
) and a recovery variable ( ), the latter of which describes the extent to which a neuron can change its voltage in time. Equilibrium points for this system are defined by the intersection of two nullclines in two-dimensional state space. Since the two neurons begin in synchronous oscillation, a limit cycle exists about the equilibrium point. The neurons may be coupled by two coupling constants, which may be either positive (excitatory) or negative (inhibitory). One of the neurons also receives an external current input. In this case, the state space for each neuron becomes three-dimensional. Only one nullcline, a cubic surface, is shown, with the trajectory of each oscillator also plotted. Interesting dynamics can be seen by varying the coupling constants, input current, and time of the trajectory. Certain attractors of the system include multiple limit cycles, stable fixed-nodes, and sometimes even chaotic dynamics.
), the latter of which describes the extent to which a neuron can change its voltage in time. Equilibrium points for this system are defined by the intersection of two nullclines in two-dimensional state space. Since the two neurons begin in synchronous oscillation, a limit cycle exists about the equilibrium point. The neurons may be coupled by two coupling constants, which may be either positive (excitatory) or negative (inhibitory). One of the neurons also receives an external current input. In this case, the state space for each neuron becomes three-dimensional. Only one nullcline, a cubic surface, is shown, with the trajectory of each oscillator also plotted. Interesting dynamics can be seen by varying the coupling constants, input current, and time of the trajectory. Certain attractors of the system include multiple limit cycles, stable fixed-nodes, and sometimes even chaotic dynamics.
Permanent Citation
"Desynchronization Dynamics of Two Coupled Oscillators"
http://demonstrations.wolfram.com/DesynchronizationDynamicsOfTwoCoupledOscillators/
Wolfram Demonstrations Project
Published: March 7 2011