Discounted Present Value

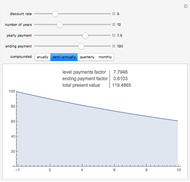
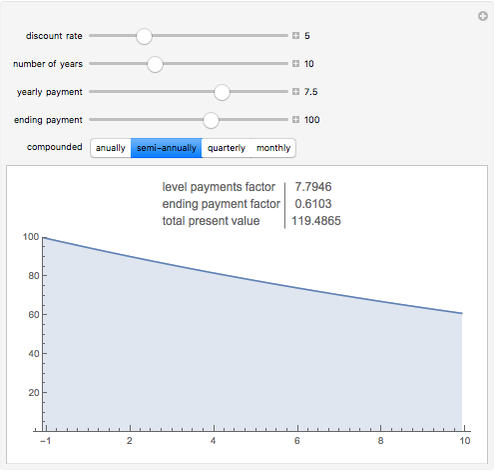
Snapshot 1: The price of a bond with a 5% coupon rate, lower than the 7% discounting rate.

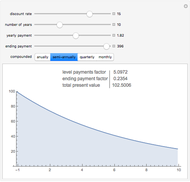
Snapshot 2: The price of a bond with a 7.5% coupon rate, higher than the 5% discounting rate.

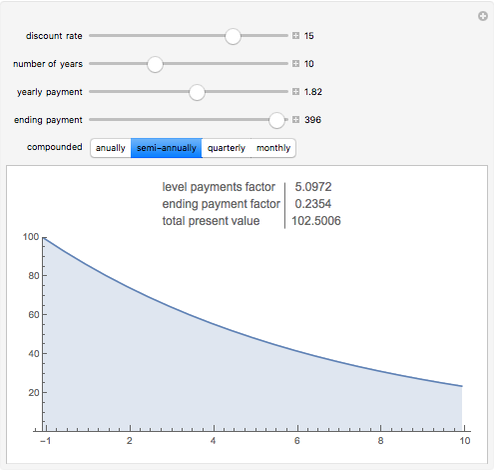
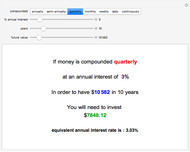
Snapshot 3: The 10-year price change a stock index paying 1.82% dividends would need to produce a 15% rate of return.

Snapshot 4: The actual return, 5.58%; the same index would pay if the price only increased by 50% over 10 years.

Snapshot 5: The break-even ending value, 37, needed to justify a long series of yearly inputs, discounted at 6%.

Snapshot 6: The internal rate of return achieved if instead the future value is 80.

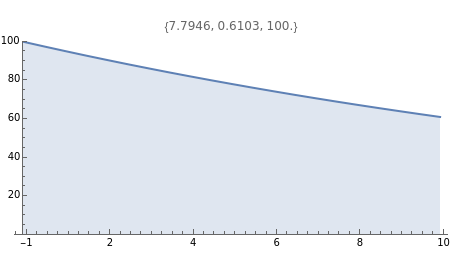
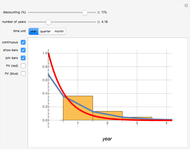
The discounted present value is the sum of the values of each of the individual cash flows, each discounted at the discount rate, for the time it occurs.

The graph shows the falling weight assigned to each cash flow, depending on its timing. The numbers in the table give the numerical total present value and its major components.

The discounted present value can be decomposed into a sum of two terms, one factor times the level payment, and another factor times the ending payment. The former is the sum of the series of discounting terms, and the latter is the last element of that series.

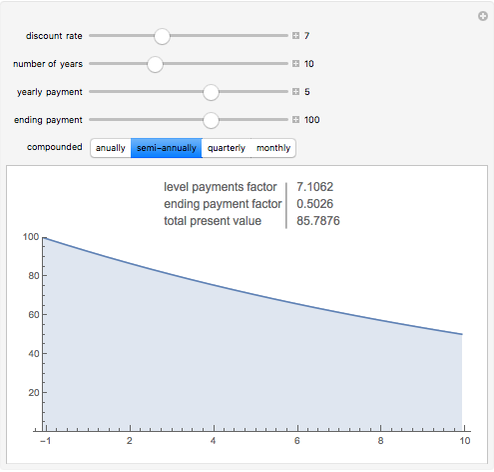
The yearly payment figure used must be an annualized figure, e.g. not a monthly payment. The compounded buttons change the discounting period used, and should be aligned
with. the actual cash flows.

Yearly compounding is appropriate for planning purposes for many projects. Bonds generally compound twice a year. Dividends are generally quarterly. Rents and mortgages are generally monthly.

When the discount rate and the yearly payments are the same, the present value is the same as the ending payment. Thus a 100 ending value bond is "at par" if the prevailing interest rate is equal to its coupon rate.

When the discount rate is higher than the yearly payments, the present value is lower then the ending payment. A bond with a low coupon is thus "at a discount".

When the discount rate is lower than the yearly payments, the present value is higher than the ending payment. A bond with a high coupon is "at a premium".

A zero payment will give the price of a zero coupon bond or the value of a single future cash flow.

Targeted rates of return from appreciating assets can be analyzed by inputing the desired return as the discount rate, and seeing what ending payment would be required to realize that rate of return.

Alternately, estimates of future value can be input as the ending payment, and the discount rate adjusted until the present value reads the amount initially invested. The discount rate that equalizes the two is the rate of return that ending value would provide.

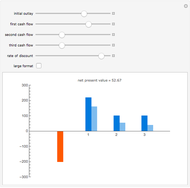
A negative level of payments can be used to determine the present value or internal rate of return of ongoing investment, returned in a lump sum value at the end.

Breakeven points between positive and negative inputs and outputs can be investigated by asking at what value of the parameters the discounted present value is zero.