Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Discrete Fourier Transform of a Two-Tone Signal

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

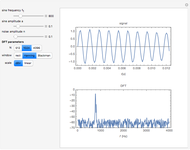
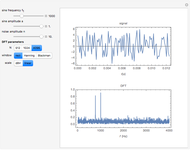
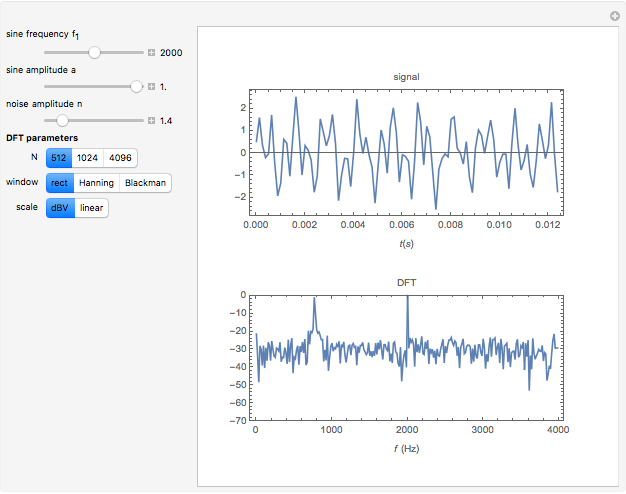
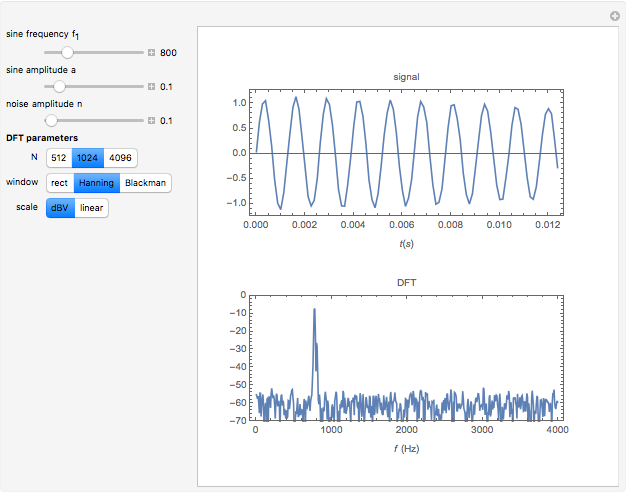
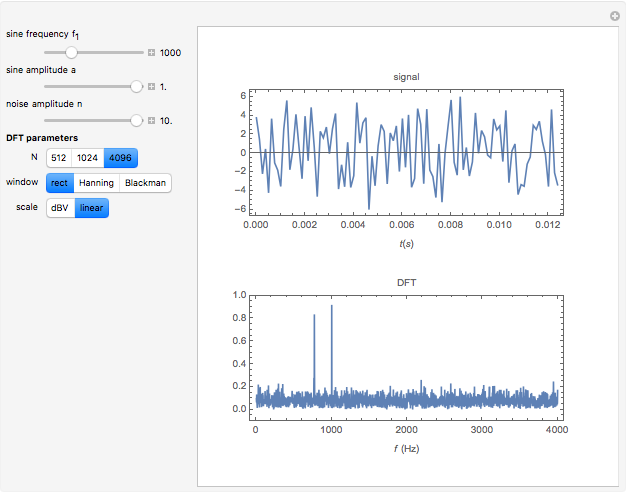
A two-tone signal is the sum of two sine waves plus a noise signal. One sine wave has the frequency 770 Hz and the amplitude 1. The frequency and the amplitude of the second sine wave as well as the noise amplitude are controlled by the sliders.

[more]

The signal is sampled at 8 kHz and the discrete Fourier transform (DFT) is calculated. The DFT is scaled such that a sine wave with amplitude 1 results in spectral line of height 1 or 0 dBV. By changing the number of samples, , and by selecting a window function, the frequency resolution and amplitude accuracy of the DFT can be examined.

[less]

Contributed by: Carsten Roppel (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The discrete-time two-tone signal is

,

where , , and is generated from a uniform distribution in the range to . You control the parameters , , and with the sliders. The -point DFT of the signal is

.

The spectrum plot shows . The factor results in a spectral line of height 1 for a sine wave of amplitude 1 if the sampling interval is an integer multiple of the sine frequency.

If a window function is applied, the signal is multiplied by before the DFT is calculated. The Hanning window is

,

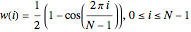and the Blackman window is

.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author

    Related Topics

Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send