Discrete Population Model for Fishery Stocks

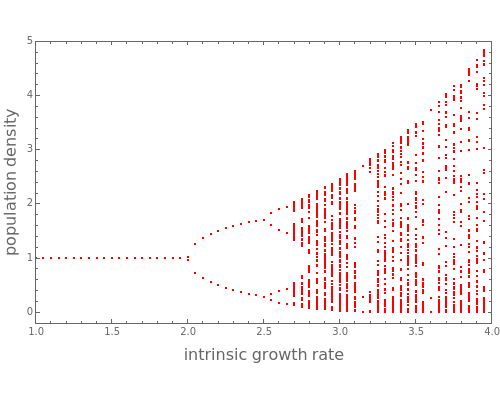
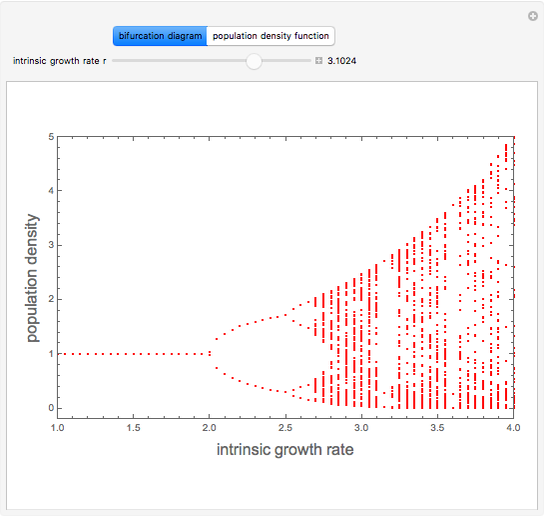
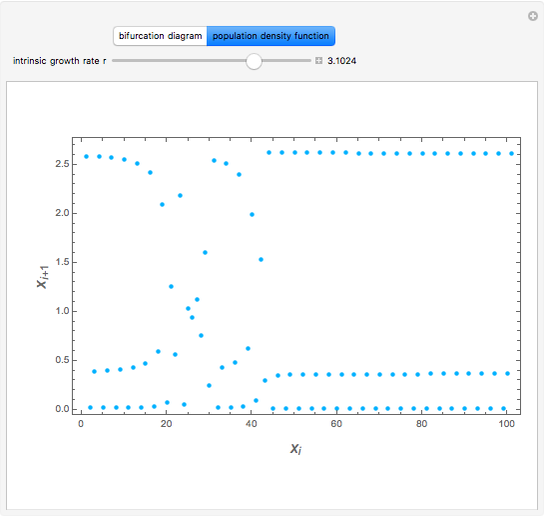
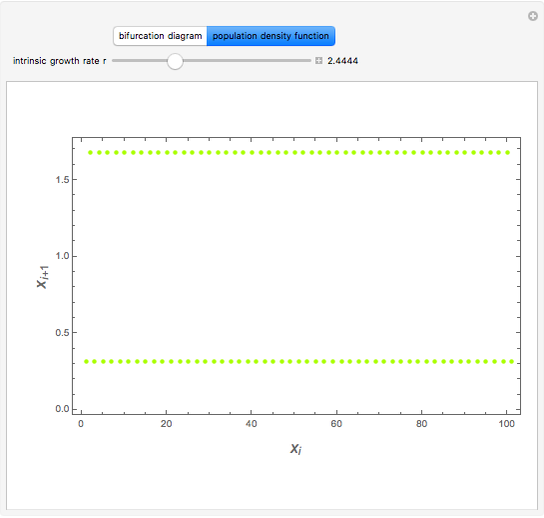
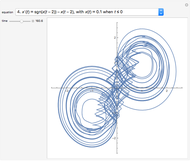
This Demonstration displays the bifurcation diagram for a realistic population dynamic model given by , where is the intrinsic growth rate (taken here as a bifurcation parameter), is the number of fish (or density of population) at generation , and is the population capacity of the environment, set equal to 1 here. This mathematical expression was given by W. E. Ricker (1954), who invented a discrete population model for fishery stocks. The model can be used to predict the number of fish in a fishery. When the cycle of period three appears, . As expected, for higher values of , we observe chaotic behavior. Snapshots 2 to 5 present period three , period two , period four , and chaotic behaviors , respectively.