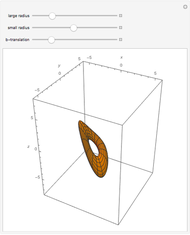
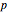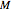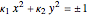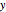Dupin's Indicatrix of a Torus
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
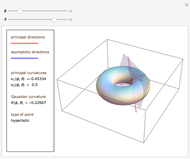
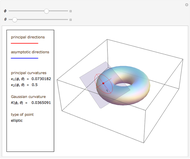
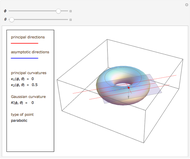
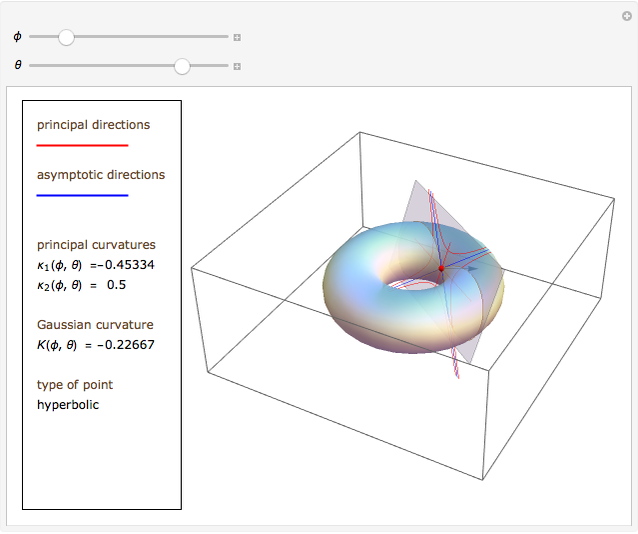
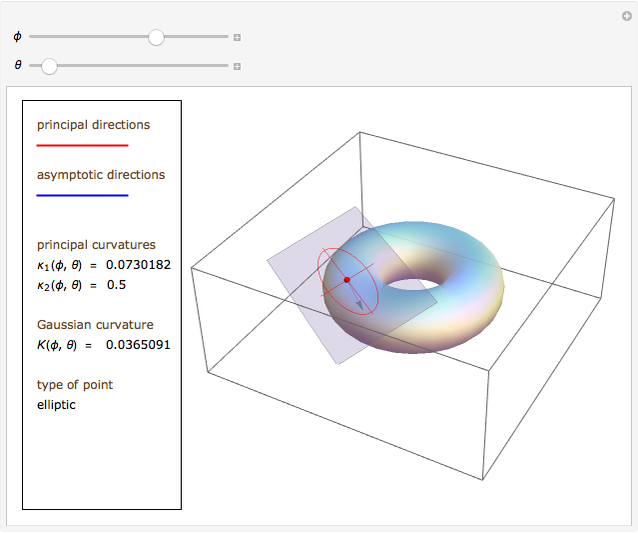
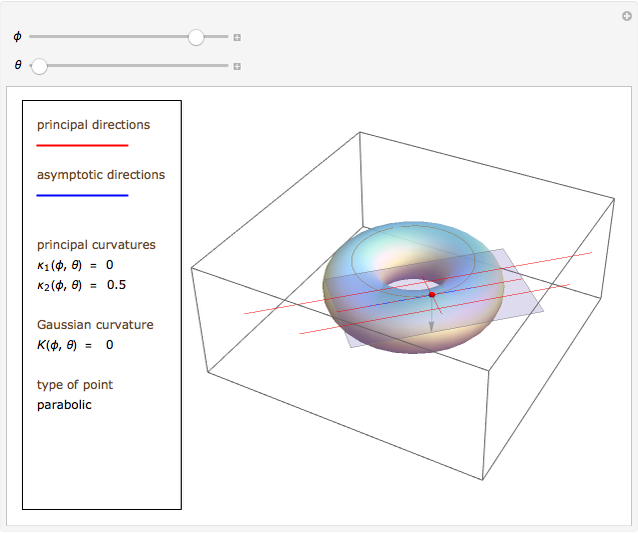
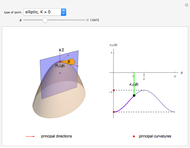
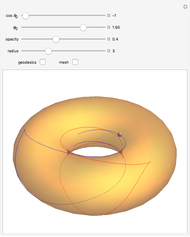
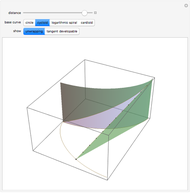
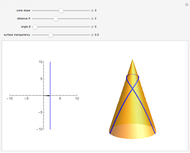
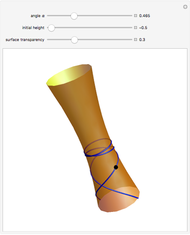
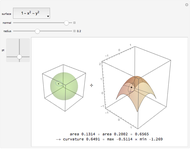
This Demonstration shows how Dupin's indicatrix changes at a variable point on a torus.
[more]
Contributed by: Sonja Gorjanc and Desana Štambuk (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation