Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dynamics of a Spring-Pendulum System

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

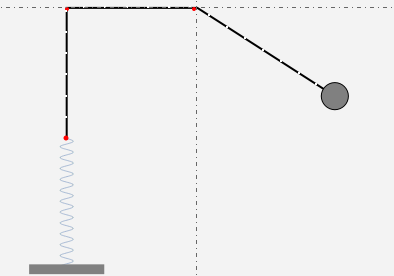
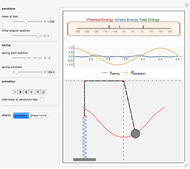
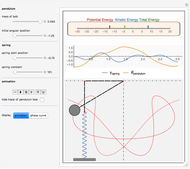
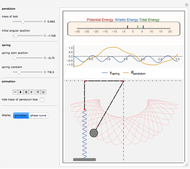
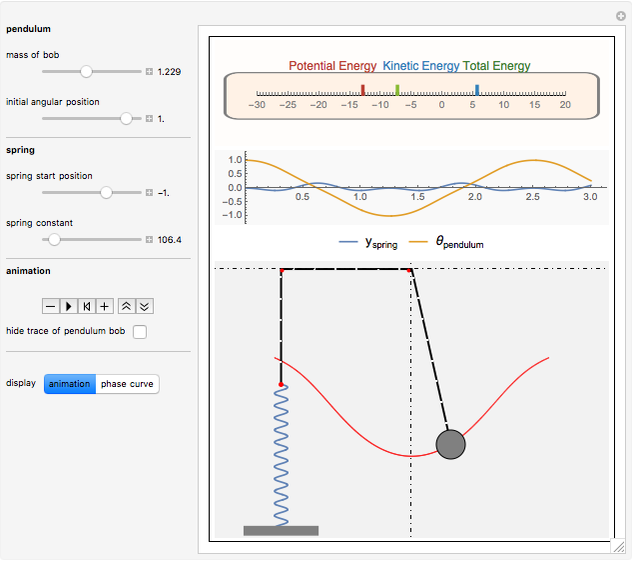
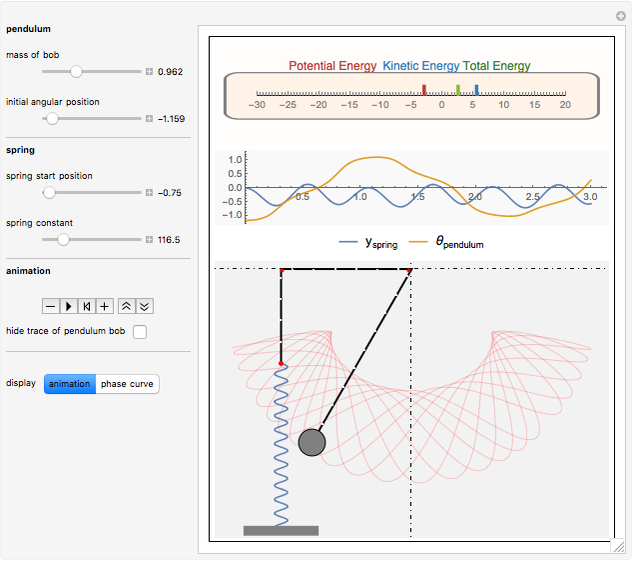
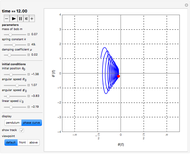
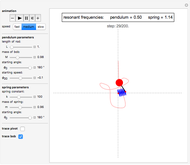
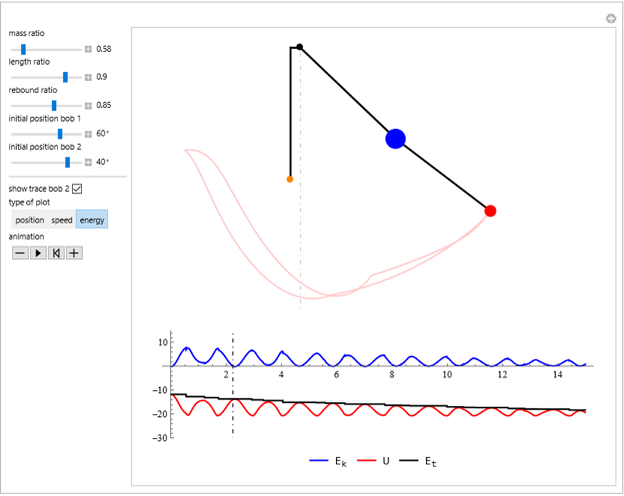
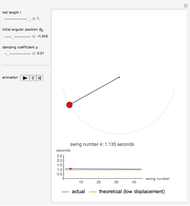
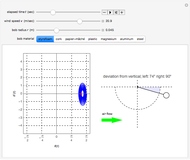
A string of fixed length is free to move over two frictionless rollers fixed at the top. A spring is at one end of the string and a bob is at the other end, forming a pendulum of variable length.

[more]

This Demonstration lets you explore the dynamics of this system by changing its parameters or initial conditions.

The chart at the top shows the conservation of energy in the system, which is utilized in the Lagrangian method to solve for the equations of motion.

[less]

Contributed by: Erik Mahieu (October 2014)
Open content licensed under CC BY-NC-SA

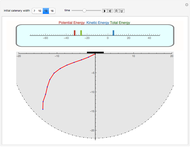
Snapshots

Details

The spring and pendulum system has two degrees of freedom: , the angular displacement of the pendulum bob, and , the vertical displacement of the spring.

Lagrangian mechanics can be used to simulate this system.

The potential energy of the system at time is:

.

The kinetic energy of the system at time is:

.

The Lagrangian is given by

.

The algebraic constraint expresses the constant length of the string:

.

The resulting equations of motion are

,

.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send