Dynamics of Three-Strategy Symmetric Games

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
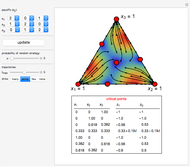
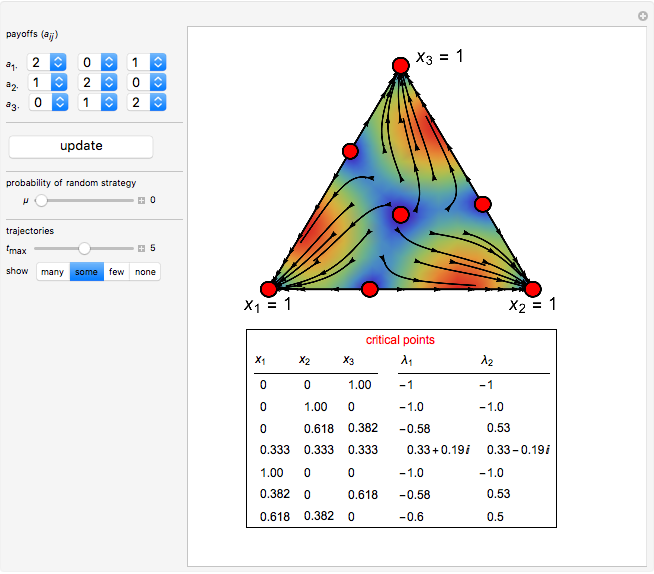
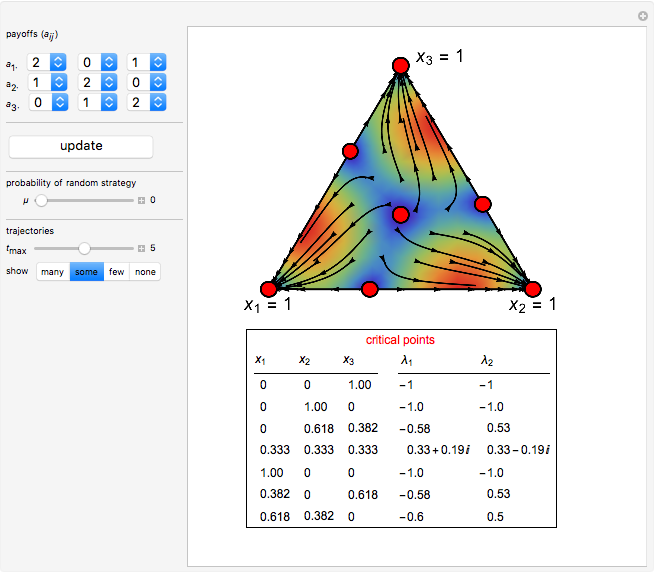
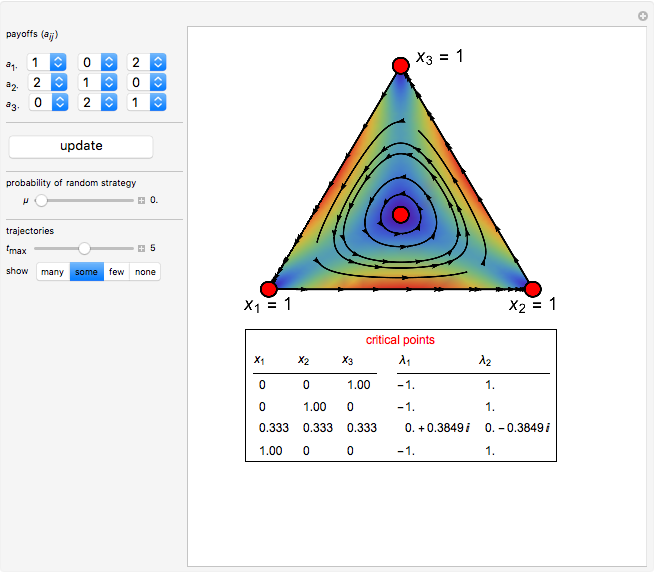
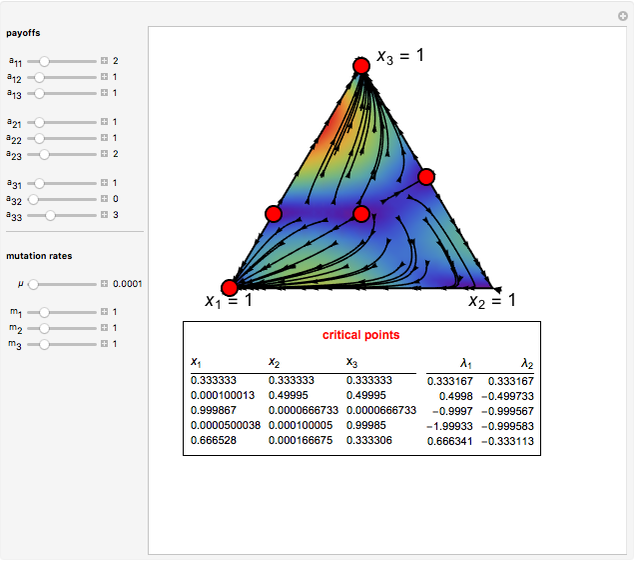
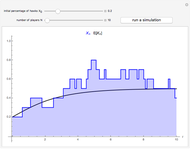
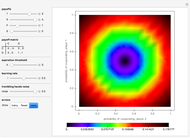
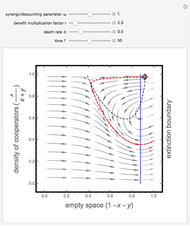
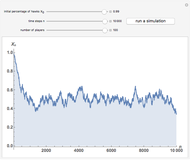
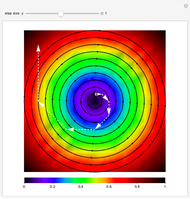
This Demonstration shows the phase portrait in the 2D simplex of the single-sampling "imitate if better" dynamics in three-strategy symmetric games for large populations.
[more]
Contributed by: Luis R. Izquierdo, Segismundo S. Izquierdo and William H. Sandholm (January 2020)
Open content licensed under CC BY-NC-SA
Details
This model is analyzed in detail in [1].
Snapshot 1: a game with seven critical points
Snapshot 2: rock paper scissors game without noise
Snapshot 3: rock paper scissors game with small noise
Snapshot 4: a game with one critical point and critical regions
Snapshot 5: a game with an internal critical region
Snapshot 6: a game with critical regions only
Reference
[1] S. S. Izquierdo and L. R. Izquierdo, "Stochastic Approximation to Understand Simple Simulation Models," Journal of Statistical Physics, 151(1–2), 2013 pp. 254–276. doi:10.1007/s10955-012-0654-z.
Snapshots
Permanent Citation