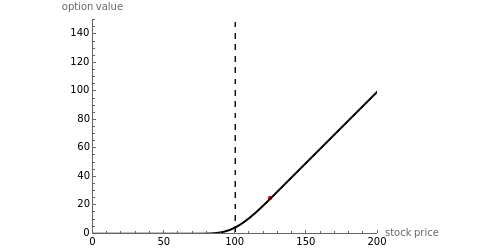
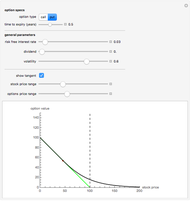
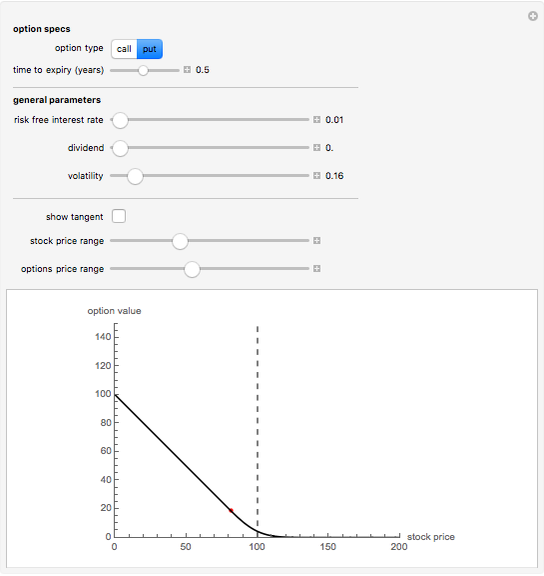
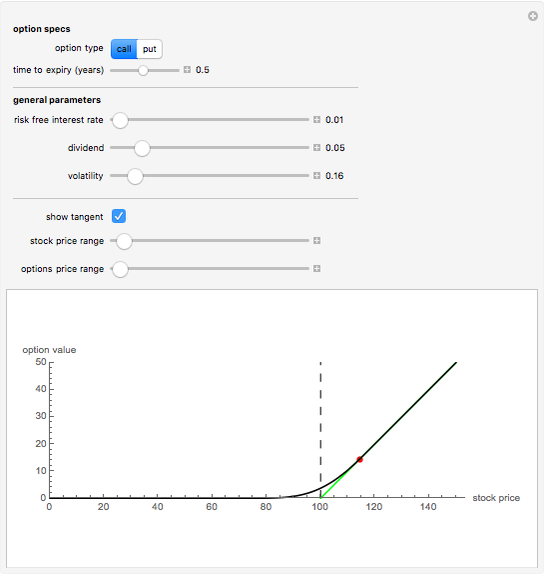
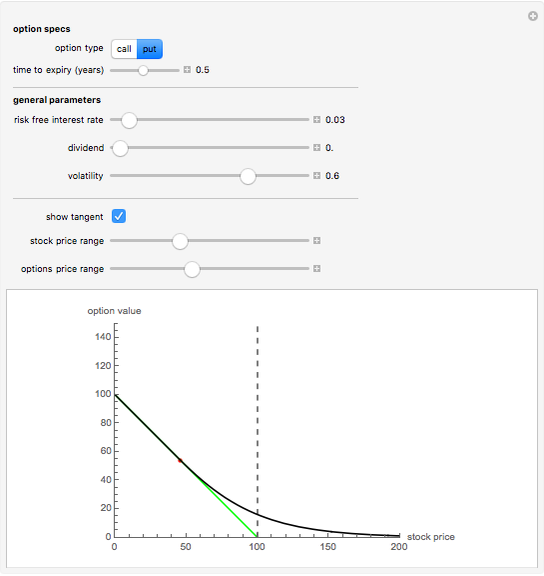
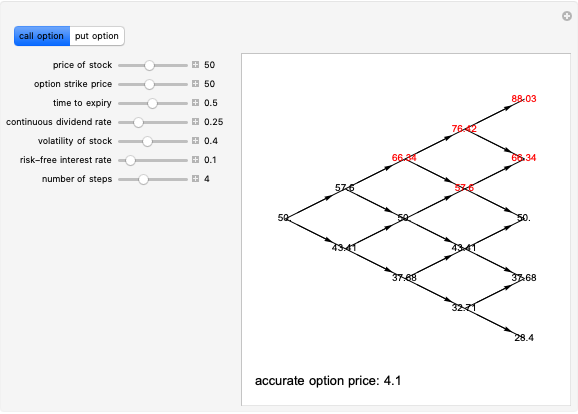
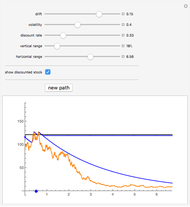
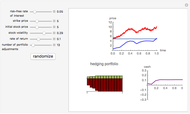
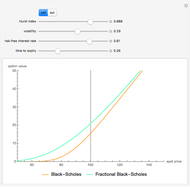
This Demonstration shows the optimal value for the exercise of an American option (call or put) in the Black–Scholes model. Unlike the European option, the American option allows early exercise. One can show that for all put options there is a price of the underlying stock such that when the stock is at (or below) this price, the option should be exercised. For call options on a stock that pays a nonzero continuous dividend, there is a stock price such that the option should be exercised when the stock price is at or above this optimal price. It is never optimal to exercise call options that pay no dividend.