Ecouter la convergence (French)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
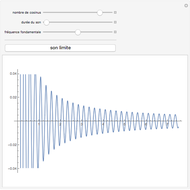
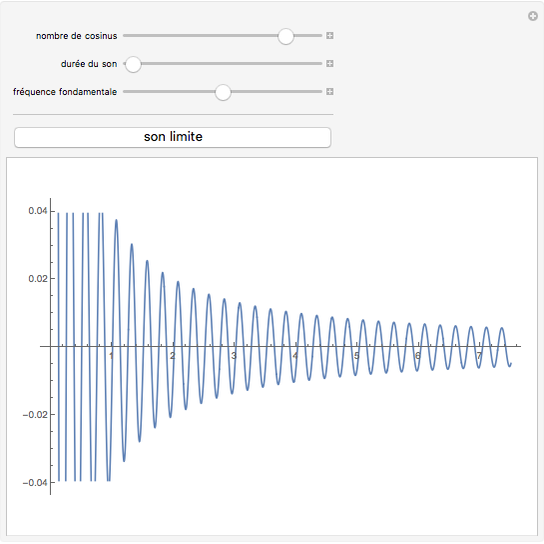
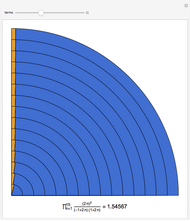
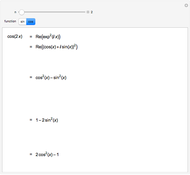
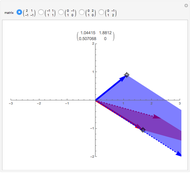
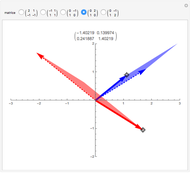
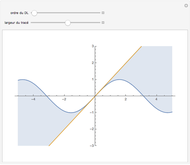
Le produit de cosinus  converge, vers une sinusoïde amortie de la forme
converge, vers une sinusoïde amortie de la forme  (sinus cardinal), quand
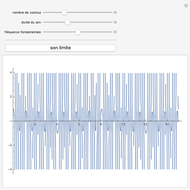
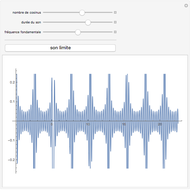
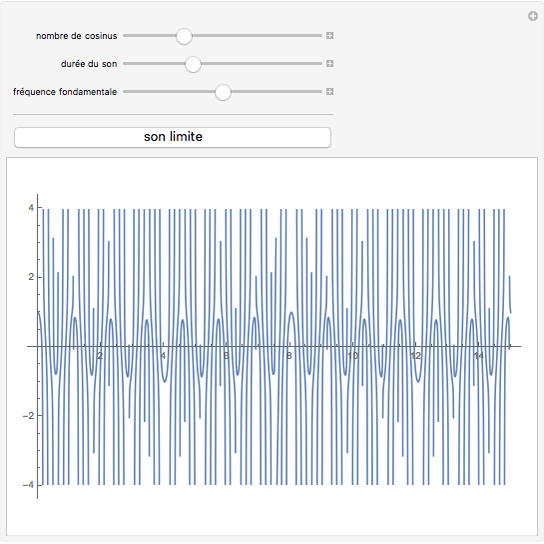
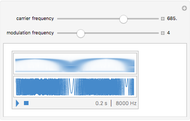
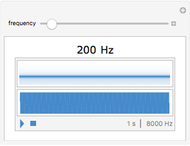
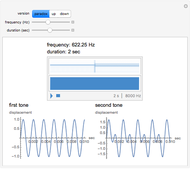
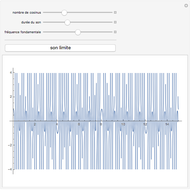
(sinus cardinal), quand  Cela peut se voir sur un graphique, mais aussi s'entendre grâce à la fonction Play. Pour entendre la fonction limite, cliquer sur le bouton "son limite". En changeant le nombre de termes du produit par le curseur "nombre de cosinus", on entend progressivement des sons de plus en plus graves, jusqu'à ce que leur fréquence passe en dessous du seuil de l'audition et devienne… une enveloppe, qui "enrobe" joliment la courbe sonore.
Cela peut se voir sur un graphique, mais aussi s'entendre grâce à la fonction Play. Pour entendre la fonction limite, cliquer sur le bouton "son limite". En changeant le nombre de termes du produit par le curseur "nombre de cosinus", on entend progressivement des sons de plus en plus graves, jusqu'à ce que leur fréquence passe en dessous du seuil de l'audition et devienne… une enveloppe, qui "enrobe" joliment la courbe sonore.
Contributed by: Emmanuel Amiot (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
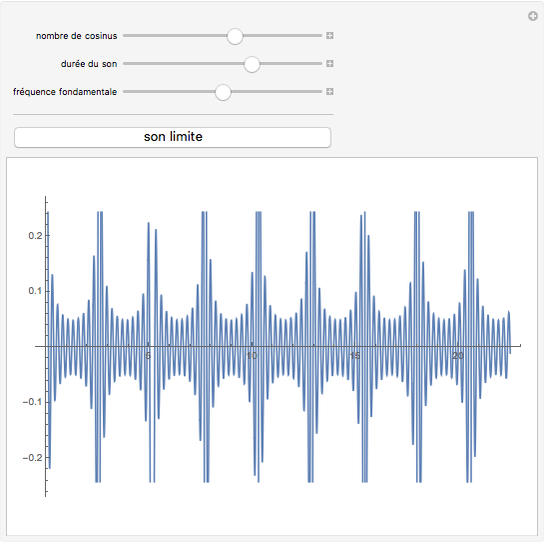
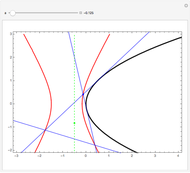
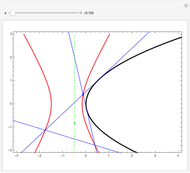
En fait, les sons produits restent périodiques (non amortis donc), mais avec une période très longue, qui double à chaque fois que l'on rajoute un cosinus dans le produit. On peut voir cette amplitude remonter, en réglant la durée totale du son au maximum, et pour une valeur du nombre de cosinus voisine de 10. Pour une durée de l'ordre d'une ou deux secondes en revanche, et avec une dizaine de cosinus, on ne peut pas faire la différence avec le sinus cardinal.
Permanent Citation
"Ecouter la convergence (French)"
http://demonstrations.wolfram.com/EcouterLaConvergenceFrench/
Wolfram Demonstrations Project
Published: March 7 2011