Effects of Temperature Fluctuations on Oscillating Biological Systems

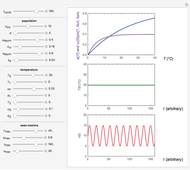
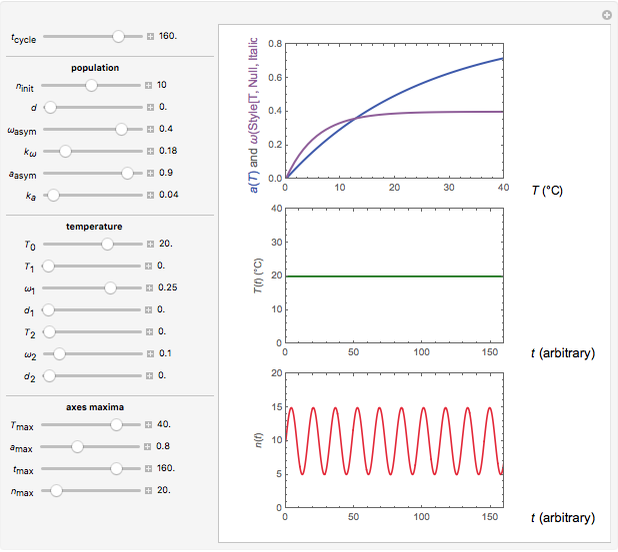
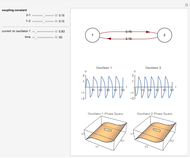
Snapshot 1: oscillation at constant temperature

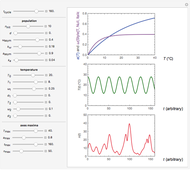
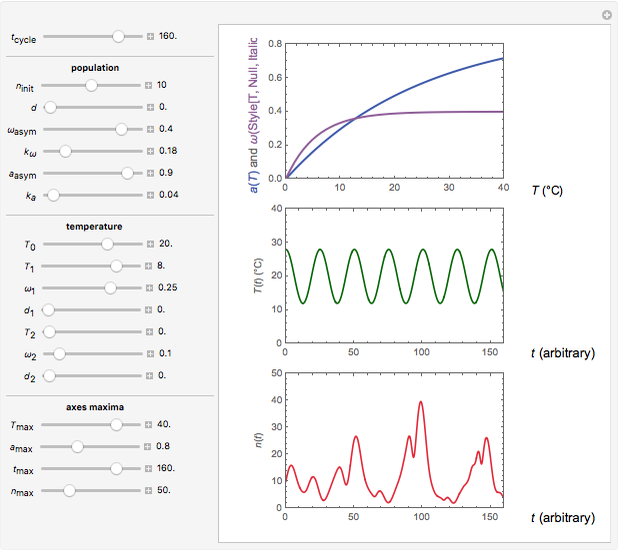
Snapshot 2: oscillation under regular temperature fluctuations

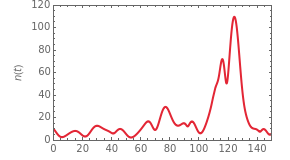
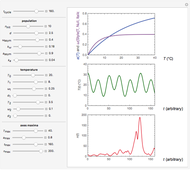
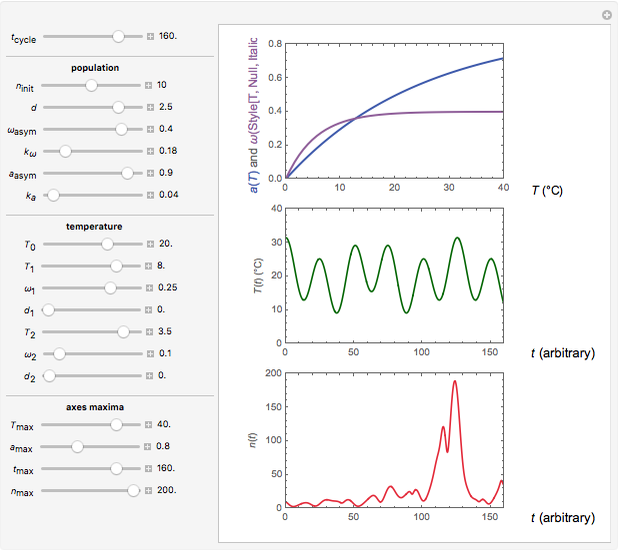
Snapshot 3: oscillation under slightly irregular temperature fluctuations leading to explosion

Snapshot 4: oscillation under slightly irregular temperature fluctuations leading to apparent extinction

Oscillating biological systems, be they organismic populations or biochemical processes, may be affected by the environment or ambient temperature, which may also fluctuate. This Demonstration illustrates the theoretical possibility that coupling a biological system's oscillations with the temperature's fluctuations can produce apparently chaotic evolution patterns such as "explosions" or a drop to a level that in nature will cause the system's extinction [1]. Such patterns can be generated with simplified models. The one used here is based on the assumption that the biological system's oscillations are single-term sinusoidal and that their amplitude and frequency rise monotonically with temperature in the pertinent temperature range. The environmental or ambient temperature fluctuations are simulated with a two-term sinusoidal model. It is assumed that the momentary rate of change in the biological system's state (e.g., population's size or bioactive compound concentration) under dynamic conditions is the momentary isothermal rate at the momentary temperature, at a time that corresponds to the system's momentary state [2].

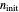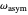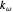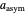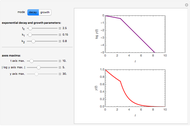
The user can choose with sliders the time, , in arbitrary units; the initial number of organisms or concentration, ; the system oscillation's phase, , in radians; and the parameters , , , and 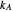, which determine the oscillation frequency's and amplitude's temperature dependence through the relationships and 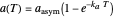, respectively, which are plotted at the top of the display.

The control parameters of the temperature's fluctuations are 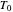, , 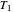, , 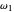, , 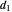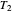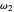and 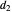, and they too can be entered with sliders. 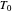, , 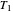and 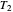are in degrees C, 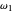and 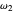in the arbitrary time unit reciprocal, a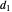nd and 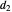in radians.

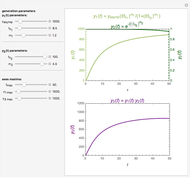
The temperature history, which is plotted in the middle of the graphical display, is generated with the model .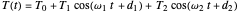

The system's evolution that corresponds to the chosen temperature fluctuation pattern and temperature dependence of the system's own oscillations is plotted at the bottom of the graphical display in the form of the 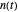versus relationship. It is calculated as the numerical solution of the differential equation 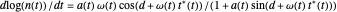, where 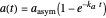, , 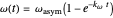and .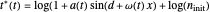

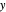Except for the time axis range, which is automatically determined by , the three plots' axes maxima can be chosen with sliders.

Note that setting 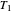and 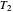to zero will simulate isothermal conditions at 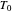, and that for a larger initial number or a smaller concentration than that allowed by the 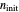slider, the result can be multiplied or divided by the appropriate factor.

Also note that the purpose of the Demonstration is just to illustrate the theoretical possibility of the emergence of different patterns. Thus, not all the simulated evolution patterns that can be generated with the allowed parameter settings necessarily have a real-life equivalent in the biological world.

References

[1] M. Peleg and M. G. Corradini, "Theoretical Effects of Monotonically Changing and Fluctuating Temperature on Oscillating Biological Systems," Ecological Complexity 7, 2010 pp. 500–505.

[2] M. Peleg, Advanced Quantitative Microbiology for Foods and Biosystems: Models for Predicting Growth and Inactivation, Boca Raton, FL: CRC Press, 2006.