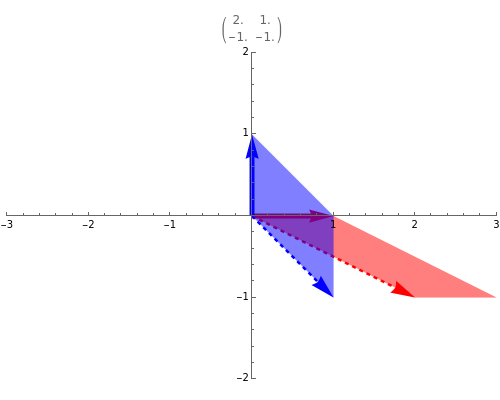
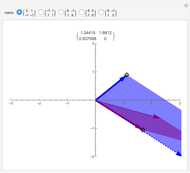
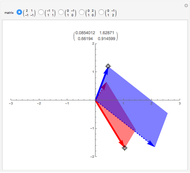
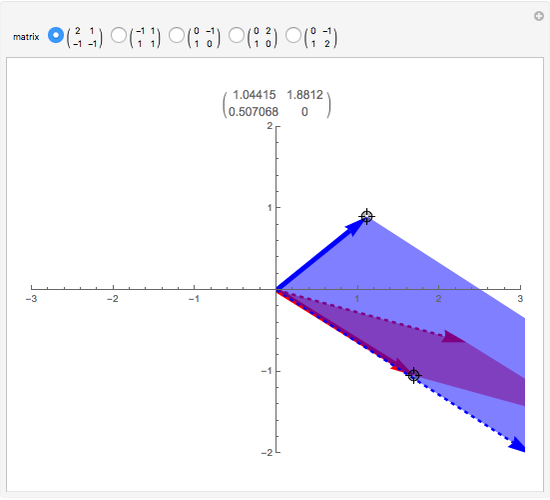
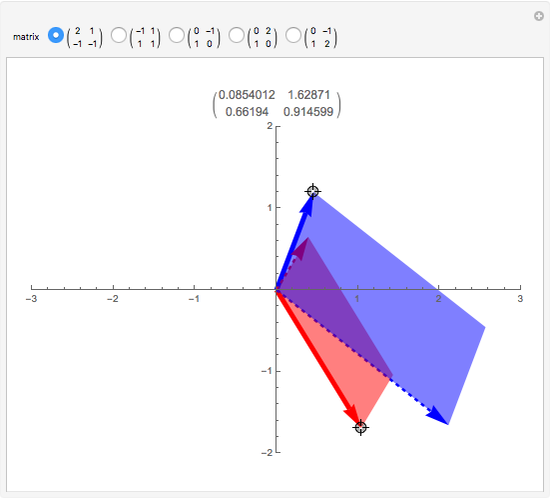
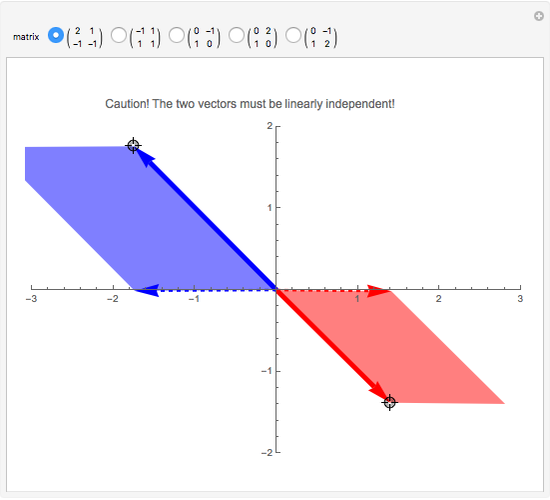
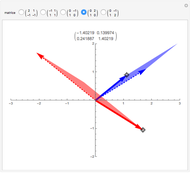
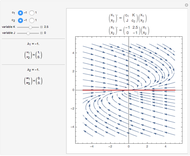
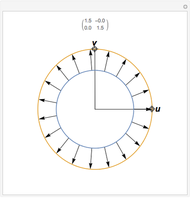
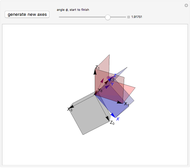
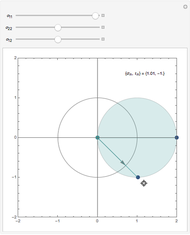
A linear map transforms vectors into other vectors. A nonzero vector (boldface in this Demonstration) is an eigenvector when its image (dotted here) is a multiple of itself; this occurs when the colored parallelogram vanishes. Drag the vectors until they become eigenvectors. If you manage to hit a basis of eigenvectors, then in this new basis the matrix of the linear map (shown above the graphic) becomes diagonal.
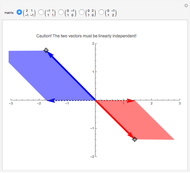
Drag each vector until the colored parallelogram vanishes. If you can do this for two independent vectors, they form a basis of eigenvectors and the matrix of the linear map becomes diagonal, that is, nondiagonal terms are zero. This is impossible for some of the initial matrices—try them all.
When you have found an eigenvector, check that it can be prolonged in its own direction while remaining an eigenvector; it is interesting to keep an eye on the matrix at the same time.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
