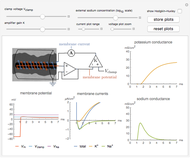
Electrodiffusion of Ions across a Neural Cell Membrane

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
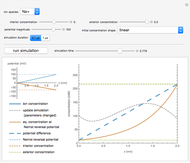
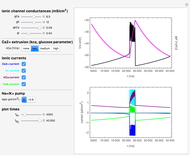
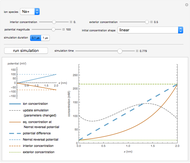
The Nernst–Planck equation describes the diffusion of ions under the influence of an electric field. Here, it is applied to describe the movement of ions across a neural cell membrane. The top half of the Demonstration sets up the simulation, while the bottom displays the results.
[more]
Contributed by: Oliver K. Ernst (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
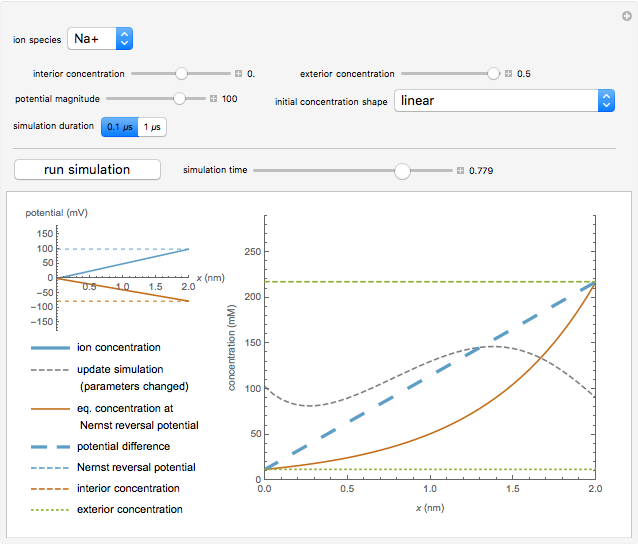
Snapshot 1: the time evolution of sodium ions from an initially linear concentration distribution
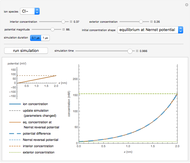
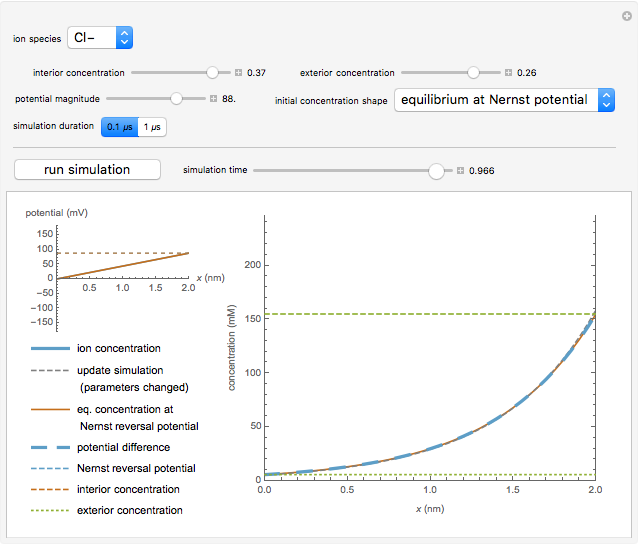
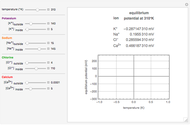
Snapshot 2: at the Nernst reversal potential, for an appropriate initial concentration distribution, the system is at equilibrium
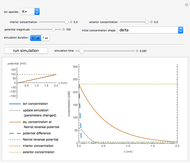
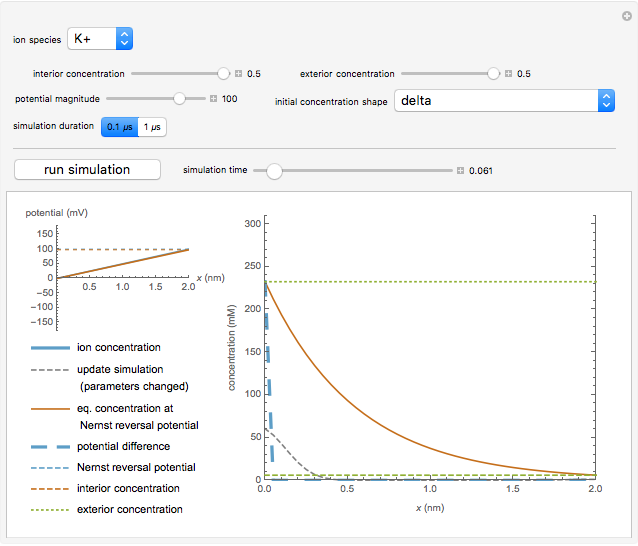
Snapshot 3: the initial delta spike of potassium ions decays as ions drift due to diffusion and the electric field
Ions undergoing diffusion in the presence of an electric field give rise to an ionic current flux 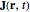 (here in units of
(here in units of 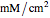 ) at position
) at position  and time
and time  as
as
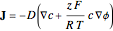 ,
,
where 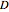 (in
(in 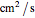 ) is the diffusion constant,
) is the diffusion constant, 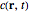 (in mM) is the ionic concentration,
(in mM) is the ionic concentration,  is the ion's charge (unitless),
is the ion's charge (unitless), 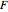 is the Faraday constant,
is the Faraday constant, 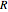 is the universal gas constant,
is the universal gas constant, 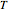 (in K) is the temperature, and
(in K) is the temperature, and 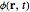 is the electric potential [1, 2]. Combined with the continuity equation
is the electric potential [1, 2]. Combined with the continuity equation
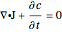 ,
,
the Nernst–Planck equation describing the evolution of the ionic concentration in time is obtained as
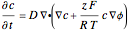 .
.
This Demonstration assumes one-dimensional motion to describe the diffusion of ions across a neural membrane. Let 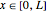 denote the direction through the membrane, perpendicular to the surface, where
denote the direction through the membrane, perpendicular to the surface, where 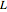 is the width of the membrane, such that
is the width of the membrane, such that  and
and 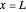 identify the interior and exterior of the neuron. Divide this distance into
identify the interior and exterior of the neuron. Divide this distance into  compartments of width
compartments of width 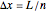 . Furthermore, discretize time into steps
. Furthermore, discretize time into steps 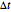 such that
such that 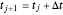 for
for 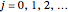 and
and  . Let
. Let 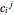 and
and 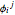 denote the constant ion concentration and potential in compartment
denote the constant ion concentration and potential in compartment 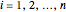 at time step
at time step 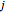 . A finite-difference approximation of the Nernst–Planck equation with zero-flux boundary conditions at the membrane boundaries is,
. A finite-difference approximation of the Nernst–Planck equation with zero-flux boundary conditions at the membrane boundaries is,
for  ,
,
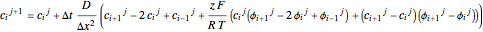 ,
,
and for  and
and 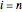 ,
,
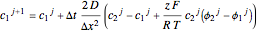 ,
,
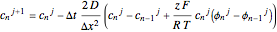 .
.
As parameter values, take the membrane width 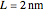 , the spacing
, the spacing 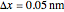 , and the temperature
, and the temperature 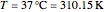 . Assume that the electric field is constant across the membrane; that is, the potential is a linear function of the distance, with a potential
. Assume that the electric field is constant across the membrane; that is, the potential is a linear function of the distance, with a potential 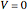 set at
set at  . The time step is chosen to satisfy the stability criteria obtained by a von Neumann stability analysis [3]
. The time step is chosen to satisfy the stability criteria obtained by a von Neumann stability analysis [3]
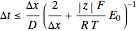 ,
,
where 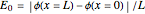 is the magnitude of the electric field.
is the magnitude of the electric field.
Four ion species may be examined, with diffusion constants taken from [1] (Table 10.1) at 25 °C in units of 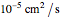 as
as
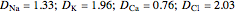 .
.
Note that these values are approximate, so that the diffusion constant can, in general, vary with temperature and across the membrane. The default values [1] (Table 1.3) of the initial interior concentrations in mM are
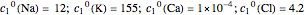 ,
,
and exterior concentrations are
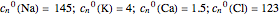 .
.
You can vary these values using the sliders that add or subtract a percentage of the default concentrations.
Three initial concentration shapes are possible:
1. The equilibrium shape at the Nernst reversal potential. If the membrane potential is also set to the Nernst reversal potential, the ionic flux is zero and the initial distribution is the equilibrium, indicated by a solid brown line.
2. A linear shape between the interior and exterior concentrations.
3. A delta function shape, with zero initial concentration everywhere across the membrane except the endpoints.
Note finally the connection between the Nernst–Planck equation and the Goldman–Hodgkin–Katz equation, which may be derived as the solution to the first differential equation above for constant ionic current flux.
References
[1] B. Hille, Ion Channels of Excitable Membranes, 3rd ed., Sunderland, MA: Sinauer, 2001.
[2] C. Koch, Biophysics of Computation: Information Processing in Single Neurons, New York: Oxford University Press, 1999.
[3] Wikipedia. "Von Neumann Stability Analysis." (Sep 23, 2015) en.wikipedia.org/w/index.php?title=Von_Neumann _stability _analysis&oldid=674227751.
Permanent Citation