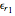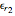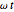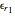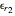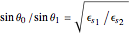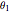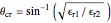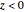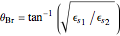Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Electromagnetic Wave Incident on a Dielectric Boundary

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

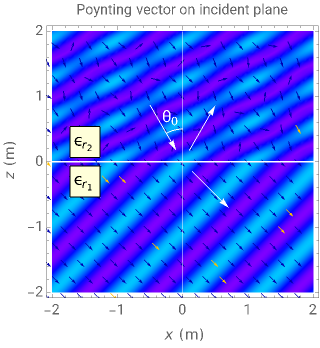
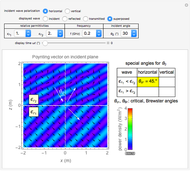
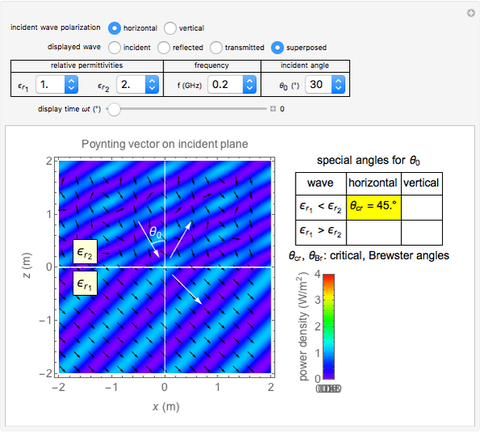
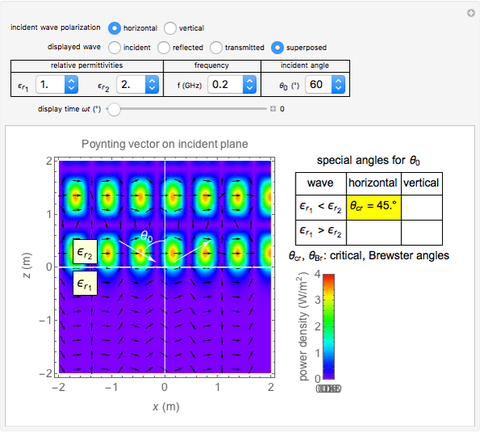
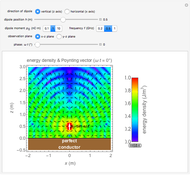
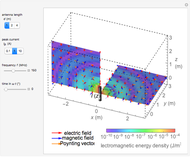
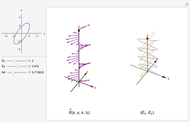
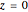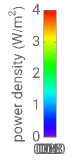
This Demonstration shows an electromagnetic wave incident on a planar dielectric boundary in terms of the Poynting vector on both sides of the boundary. Taking the incident plane and boundary planes to be and , respectively, the resulting Poynting vector pattern is shown on the incident - plane. The incident wave is assumed to be linearly polarized either horizontally or vertically with respect to the electric field. (The horizontal wave and vertical wave are sometimes called the p-wave and s-wave, respectively.) In all the cases, the power density (Poynting vector intensity) of the incident wave is set to 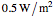on average, that is, to peak at.

[more]

You can set the frequency (in the range 0.1–0.5 GHz), permittivities and (in the range 1–5), and the incident angle (in the range 0–90°). You can set the time of display (phase) and you can vary the time automatically.

Let the relative permittivities of the lower and upper dielectrics be and . Snell's law holds: , where and are incident and transmitted angles. The reflection angle is equal to . The critical angle can be defined in the case . Snapshots 1 and 2 correspond to the cases and , respectively. The latter is the case of total reflection, in which the transmitted angle is complex. Calculations using the complex angle give diminishing fields in the region . In the case of a vertically polarized incident wave, the Brewster angle is . No reflections occur for , which is shown in Snapshot 3. Those special angles, if any, are shown in the table on the right.

[less]

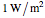Contributed by: Y. Shibuya (October 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

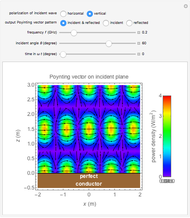
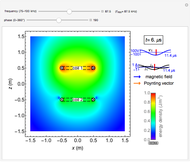
Snapshot 1: horizontally polarized incident wave with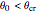

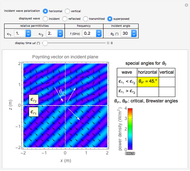
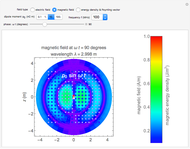
Snapshot 2: horizontally polarized incident wave with 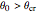; the case of total reflection

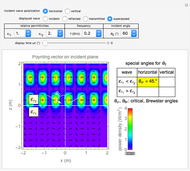
Snapshot 3: vertically polarized incident wave with 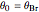; the case of no reflection

According to Fresnel's equations for the horizontally polarized incident wave's electric field 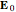, transmitted and reflected fields are expressed by 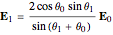and 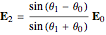. Similar calculations can be made for the vertically polarized incident wave.

Generally, the upper half-space accommodates two waves: incident and reflected; therefore, the Poynting vector pattern is made up of undulating patterns. On the other hand, the lower half accommodates the transmitted wave only, showing a straight plane wave, provided 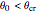. In the special case of Snapshot 3, the upper space shows the pattern of one plane wave, since there is no reflected wave.

Reference

[1] J. A. Stratton, Electromagnetic Theory, New York: McGraw-Hill, 1941 pp. 483–600.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send