Energies for Particle in a Gaussian Potential Well

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
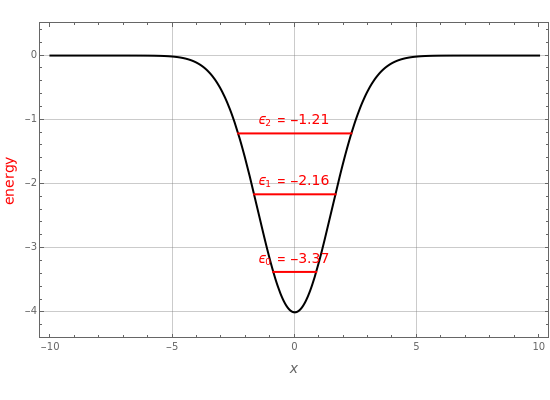
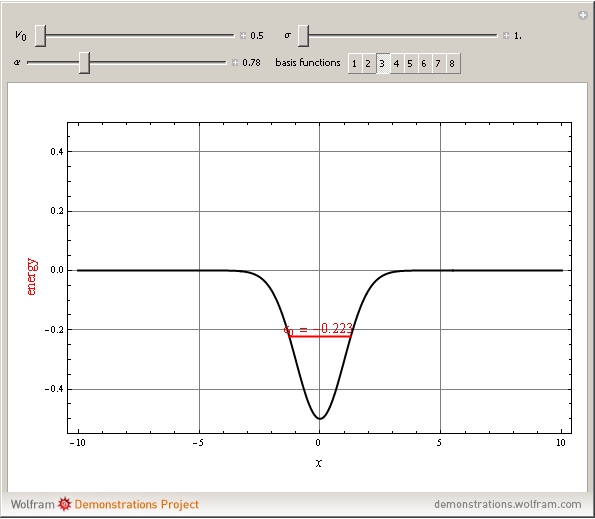
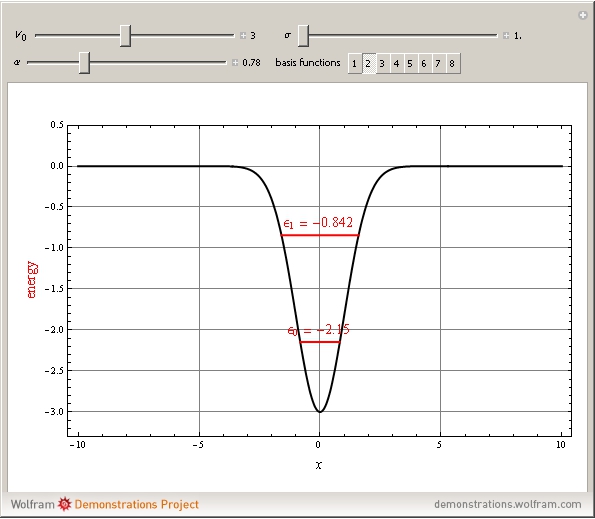
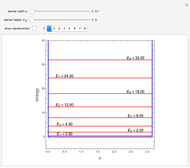
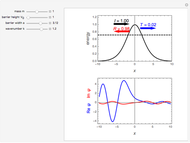
The Schrödinger equation for a particle in a one-dimensional Gaussian potential well  , given by
, given by  , has never been solved analytically. This Demonstration derives an approximation for the first few bound-state energies,
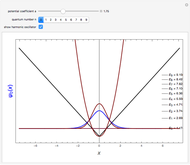
, has never been solved analytically. This Demonstration derives an approximation for the first few bound-state energies,  , using the linear variational method. The wavefunction is approximated by a linear combination
, using the linear variational method. The wavefunction is approximated by a linear combination  . It is convenient to take the basis functions
. It is convenient to take the basis functions  as the corresponding orthonormalized eigenfunction of the linear harmonic oscillator:
as the corresponding orthonormalized eigenfunction of the linear harmonic oscillator:  , where
, where  is the
is the  Hermite polynomial and
Hermite polynomial and  is a scaling constant to be determined variationally. After evaluating the matrix elements
is a scaling constant to be determined variationally. After evaluating the matrix elements  over the selected set of
over the selected set of  basis functions, Mathematica can calculate the
basis functions, Mathematica can calculate the  eigenvalues in a single step, from which we select only those with negative values. For convenience, we set
eigenvalues in a single step, from which we select only those with negative values. For convenience, we set  , so that all distances are expressed in bohrs (Bohr radii) and energy quantities in hartrees.
, so that all distances are expressed in bohrs (Bohr radii) and energy quantities in hartrees.
Contributed by: S. M. Blinder (August 2012)
Open content licensed under CC BY-NC-SA
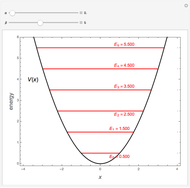
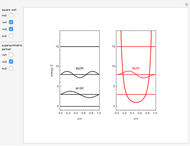
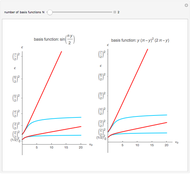
Snapshots
Details
Reference:
D.A. McQuarrie, Quantum Chemistry, Sausalito, CA: University Science Books, 1983, pp. 266-275. Or numerous other texts on quantum mechanics or quantum chemistry.
Permanent Citation