Energy Levels and Wavefunctions of Two Coupled Atomic Rings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
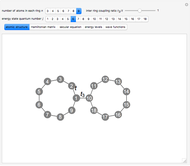
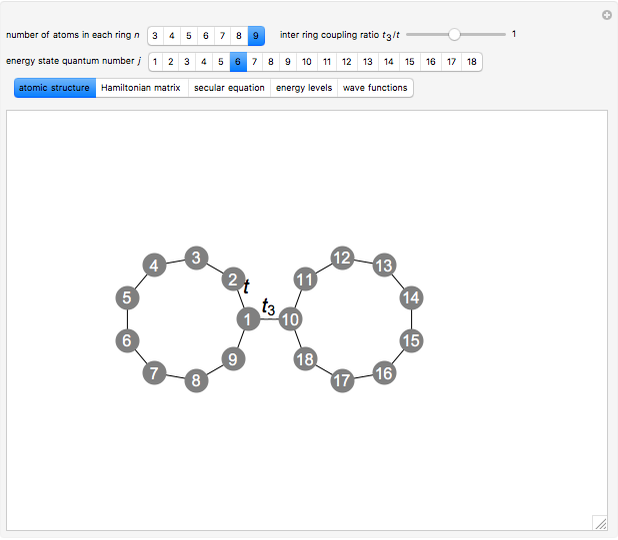
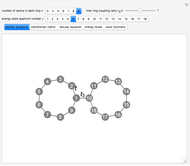
This Demonstration explores the quantum-mechanical system of two atomic rings coupled in biphenyl molecule-like geometry, within the tight-binding model. The energy levels and wavefunctions of the two coupled rings are determined from the secular equation. Analytical treatment of the problem is simplified to a 2x2 block structure of the Hamiltonian matrix, from a suitable choice of the atomic-site enumeration. The signs of the wavefunction on all the atoms is shown, yellow for positive and green for negative.
Contributed by: Vasil Saroka (September 2018)
Open content licensed under CC BY-NC-SA
Details
Within the nearest-neighbor approximation, the tight-binding Hamiltonian matrix for the two coupled atomic rings has a 2x2 block structure
 .
.
The eigenproblem for this Hamiltonian can be reduced to two eigenproblems of  by
by  matrices
matrices  , where
, where  is the number of atoms in each ring. The tridiagonal structure of such matrices allows one to treat their eigenproblems by the transfer matrix method [1].
is the number of atoms in each ring. The tridiagonal structure of such matrices allows one to treat their eigenproblems by the transfer matrix method [1].
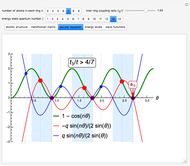
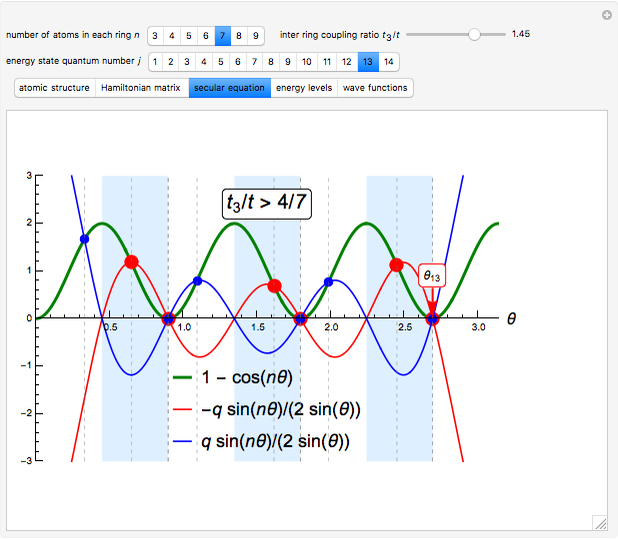
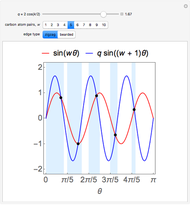
The resulting secular equation for the given system reads
 ,
,
where  is the number of atomic sites in each ring;
is the number of atomic sites in each ring;  is the electron momentum, quantized by the secular equation;
is the electron momentum, quantized by the secular equation;  and
and 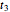 are the tight-binding hopping integrals for electron hoppings within and between the rings, respectively; and
are the tight-binding hopping integrals for electron hoppings within and between the rings, respectively; and  is a parameter specifying the symmetry of the electronic wavefunctions.
is a parameter specifying the symmetry of the electronic wavefunctions.
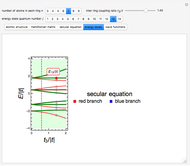
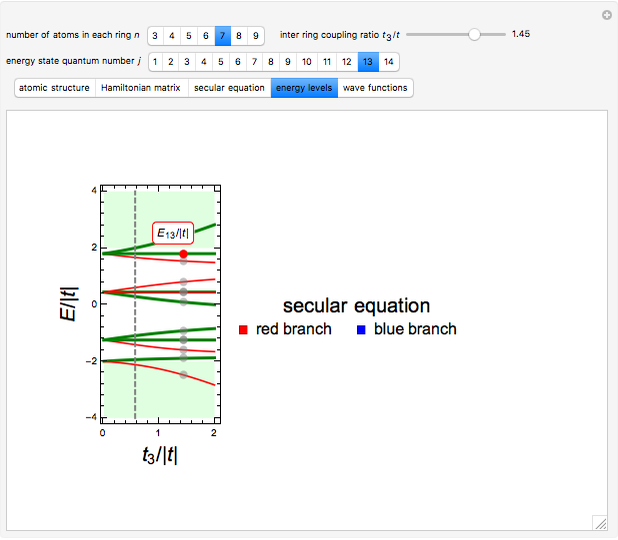
The energy levels of the system are given by
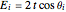 ,
,
where  is the
is the 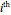 solution of the above secular equation.
solution of the above secular equation.
Note that for  (blue branch of the secular equation), the wavefunctions are always symmetric with respect to the reflection in the plane that is normal to the coupling bond and intersects it in the middle while for
(blue branch of the secular equation), the wavefunctions are always symmetric with respect to the reflection in the plane that is normal to the coupling bond and intersects it in the middle while for  (red branch of the secular equation), such symmetry is broken.
(red branch of the secular equation), such symmetry is broken.
Snapshot 1: the solutions of the secular equation of two coupled atomic rings for  and
and 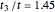
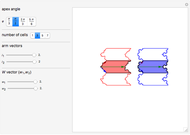
Snapshot 2: the energy levels of the system presented as a function of the coupling strength 
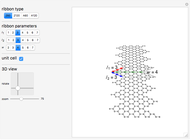
Snapshot 3: the wavefunction (eigenvector) of the two coupled rings for  and
and 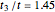
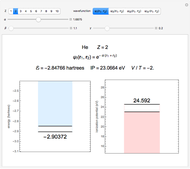
For  , we have benzene rings so that the system is an actual biphenyl molecule. The energy levels of the biphenyl (or diphenyl) molecule has been treated by an expansion of the determinant generating function [2, 3].
, we have benzene rings so that the system is an actual biphenyl molecule. The energy levels of the biphenyl (or diphenyl) molecule has been treated by an expansion of the determinant generating function [2, 3].
The transfer matrix method also applies to the problem of two coupled carbon nanotubes or graphene nanoribbons, which are promising materials for THz application [4]. An example of a single tube and ribbon treated by the transfer matrix method can be found in [5].
References
[1] V. A. Saroka, "Analytical Solutions for Energies and Wavefunctions of Two Coupled Quantum Rings in Tight-Binding Model," in Actual Problems of Radiophyics, Proceedings of the VII International Conference “APR–2017”, Tomsk, Russia, London: Red Square Scientific, 2018 pp. 5–9. books.google.ru/books?id=QsBdDwAAQBAJ&pg=PA5&hl=ru&source=gbs_toc _r&cad=3#v=onepage&q&f=false.
[2] J. E. Lennard-Jones, F. R. S. and J. Turkevich, "The Electronic Structure of Some Polyenes and Aromatic Molecules. II–The Nature of the Links of Some Aromatic Molecules," Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 158(894), 1937 pp. 297–305. doi:10.1098/rspa.1937.0021.
[3] C. A. Coulson, "The Electronic Structure of Some Polyenes and Aromatic Molecules. IV. The Nature of the Links of Certain Free Radicals," Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 164(918), 1938 pp. 383–396. doi:10.1098/rspa.1938.0024.
[4] M. E. Portnoi, V. A. Saroka, R. R. Hartmann and O. V. Kibis, "Terahertz Applications of Carbon Nanotubes and Graphene Nanoribbons," in 2015 IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, IEEE 2015 pp. 456–459. doi:10.1109/ISVLSI.2015.97.
[5] V. A. Saroka, M. V. Shuba and M. E. Portnoi, "Optical Selection Rules of Zigzag Graphene Nanoribbons," Physical Review B, 95(15), 2017 155438. doi:10.1103/PhysRevB.95.155438.
Snapshots
Permanent Citation