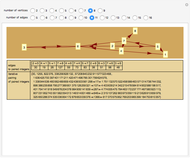
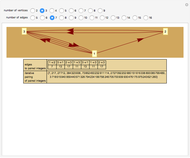
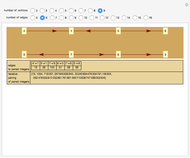
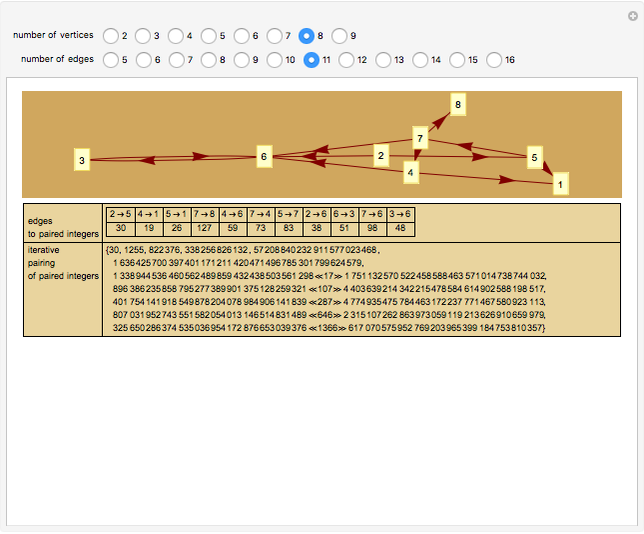
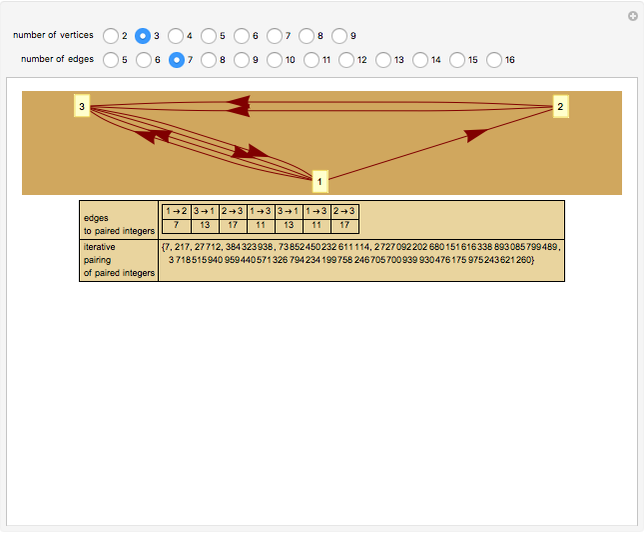
A directed graph can be described as a list of ordered pairs of positive integers denoting the edges; the integers denote the vertices. But a pair of integers can be collapsed into a unique single integer using a pairing function. Moreover, this transformation of a pair can be inverted. This means that a directed graph can be uniquely described by a single integer obtained by (a) converting the ordered pairs into a single number and then (b) iteratively pairing those paired integers using the pairing function. The process can be reversed and the edges recovered so long as one knows how many edges the directed graph had to begin with.
This Demonstration illustrates this concept. You constrain the number of vertices and edges for the directed graph. The Demonstration responds by generating a random graph that satisfies the constraint and showing the process generating the integer representation of this graph. The last number in the listing of the iterative pairing of paired integers is the unique integer identifier for the graph. Even for these relatively small graphs, this integer may contain tens of thousands of digits and is thus displayed in shortened form.
Browse all topics
