Estimating the Contraction of a Cooled Cylinder Assuming a Constant Coefficient of Thermal Expansion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
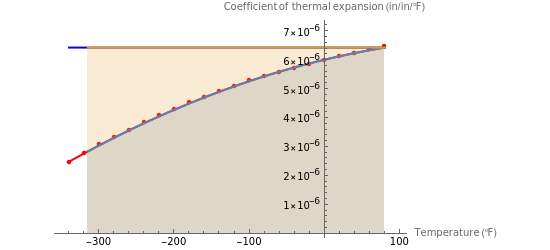
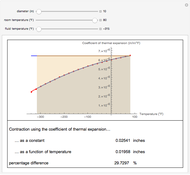
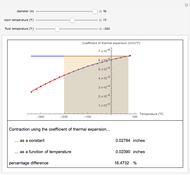
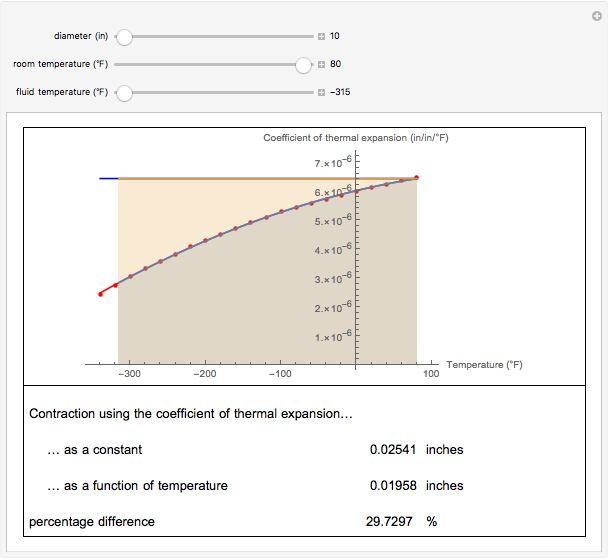
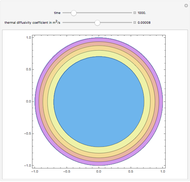
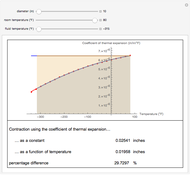
In the contraction of a hot steel cylinder immersed in a cooler medium, the coefficient of thermal expansion of steel decreases with temperature. Assuming that the coefficient of thermal expansion is constant can result in an overestimation or underestimation of the magnitude of the contraction. This Demonstration shows the possible variation between the two estimates.
Contributed by: Vincent Shatlock and Autar Kaw (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
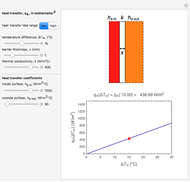
Immersing metal parts in a cool medium is used consistently in shrink-fit assemblies. To calculate the contraction in these metal parts, one needs to know the thermal expansion coefficient of the metal, the original dimensions of the part, and the temperature change. For example, if one immerses a solid cylinder that is at room temperature in cool medium such as dry ice/alcohol or liquid nitrogen, the reduction in the outer diameter of the cylinder can be calculated as
 , (1)
, (1)
where:
 outer diameter of the cylinder,
outer diameter of the cylinder,
 coefficient of thermal expansion coefficient at room temperature,
coefficient of thermal expansion coefficient at room temperature,
 temperature of cool medium
temperature of cool medium
 room temperature
room temperature
However, the coefficient of thermal expansion of steel varies considerably with temperature, as shown in this table:

The contraction in the diameter of the cylinder for the case where the thermal expansion coefficient varies as a function of temperature is given instead by
 . (2)
. (2)
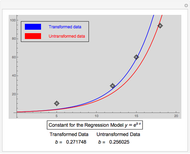
One way to find the contraction in the diameter is to fit the coefficient of thermal expansion versus temperature data by using polynomial regression. In this case, we fit a second-order polynomial  .
.
Then
 ,
,
 (3)
(3)
In this Demonstration, we show the difference in estimating the diameter contraction by using Equations (1) and (2). We try to answer the following questions:
1. Does the relative difference increase as one chooses cooler media for contraction? 2. Which equation underestimates the amount of contraction? 3. To use Equation (2), what are the results if one uses the trapezoidal rule with unequal segments?
References
[1] A. Kaw and A.Yalcin, "Problem-Centered Approach in a Course in Numerical Methods," ASCE Journal of Professional Issues and Engineering Education, 134(4), 2008 pp. 359–364.
[2] A. Kaw and E. Kalu, Numerical Methods with Applications. (Feb 18, 2011) http://numericalmethods.eng.usf.edu/publications_book.html.
Permanent Citation