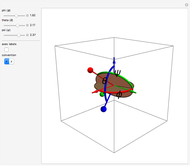
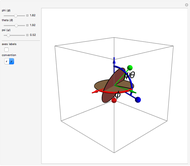
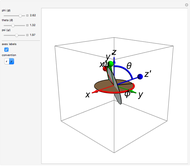
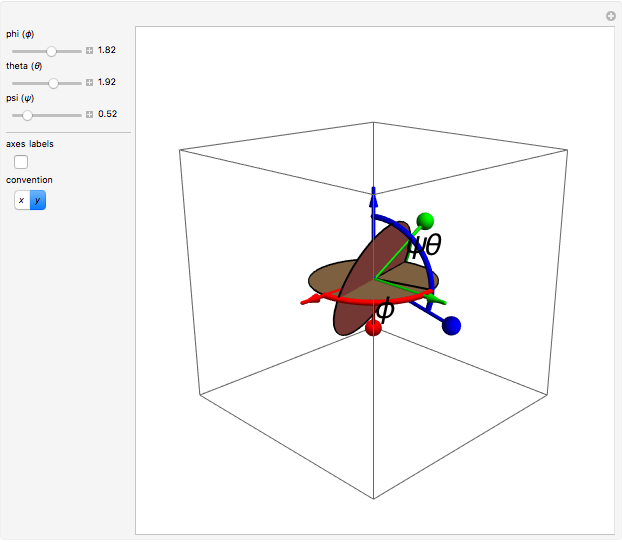
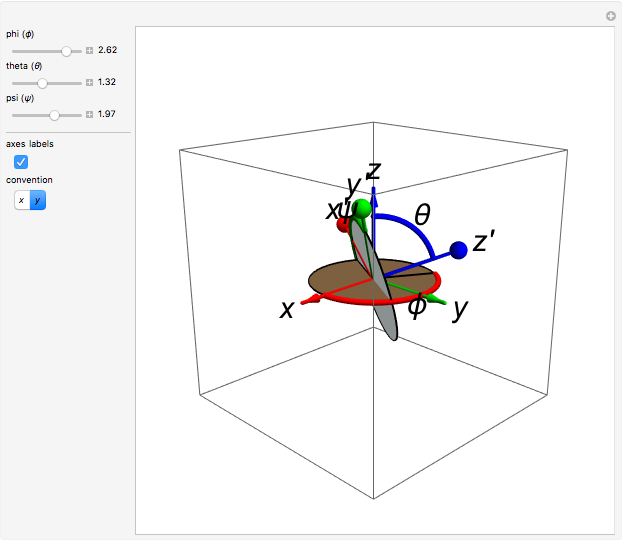
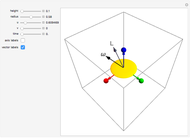
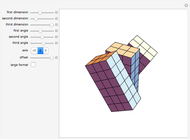
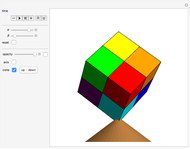
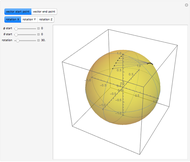
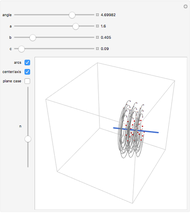
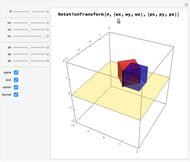
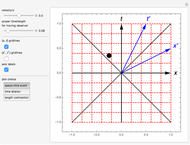
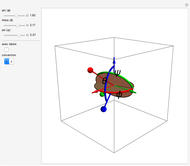
The Euler angles are a classical way to specify the orientation of an object in space with respect to a fixed set of coordinate axes. This Demonstration shows two of the several implementations of the Euler angles 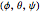. The initial 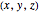axes are indicated by the red, green, and blue arrows, while the final 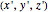axes are indicated by the red, green, and blue spheres.
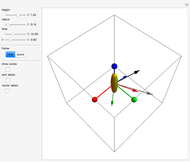
The Euler angles 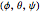are used to define a sequence of three rotations 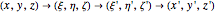, by the angles 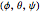about the , , or , and 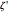axes, respectively. If the second rotation is about the axis, this is called the " convention". The net transformation is given by the matrix equation
.
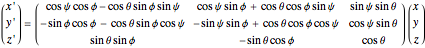This convention is used by Thornton and Marion [1] in Chapter 11.
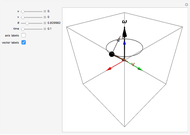
If the second rotation is about the axis, this is called the "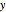 convention". The net transformation is given by the matrix equation
.
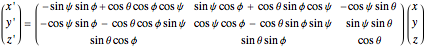This convention is used by J. R. Taylor [2] in Chapter 10.
Both conventions are described by H. Goldstein [3] in Chapter 4.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
