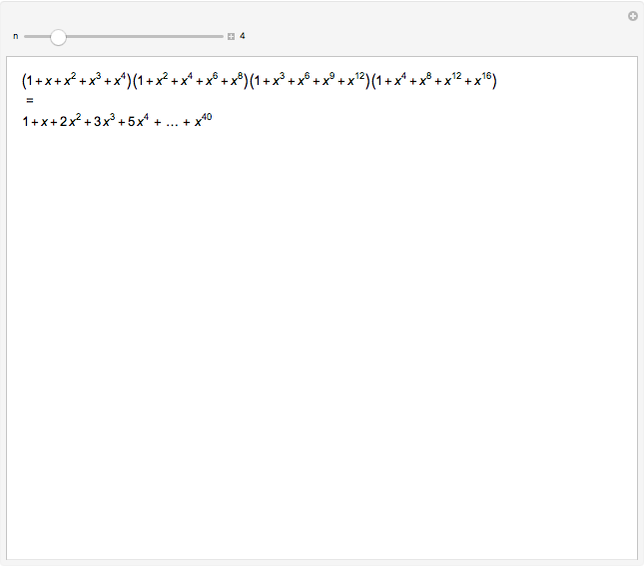
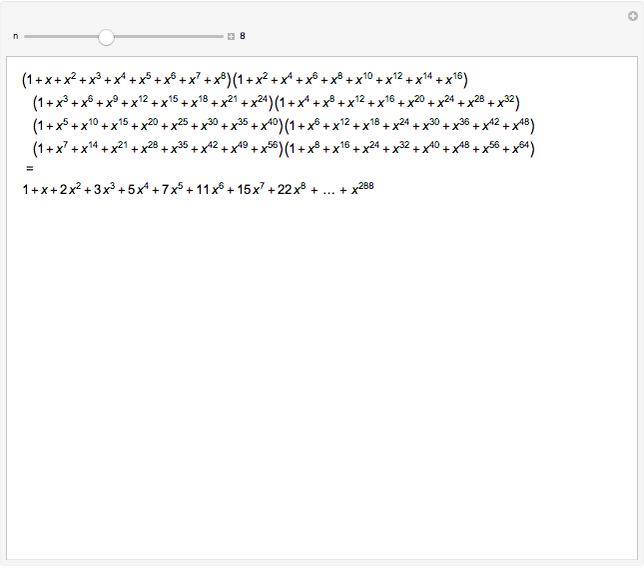
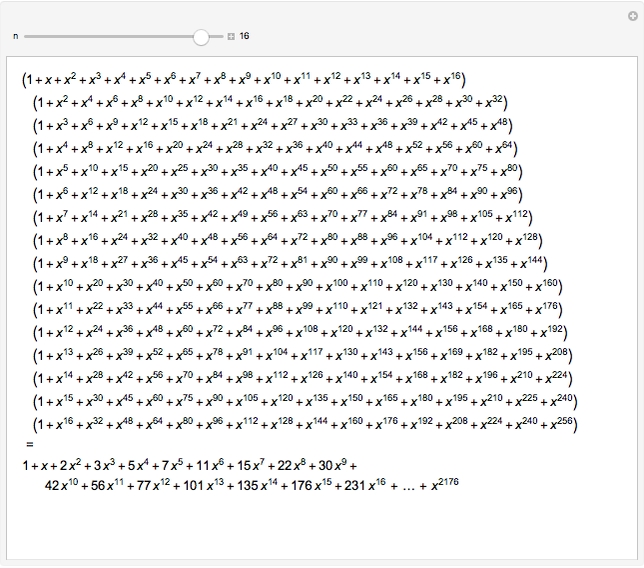
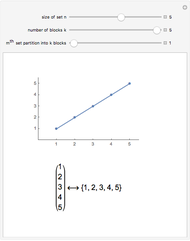
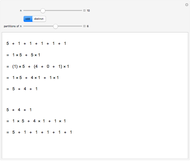
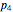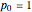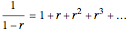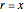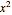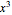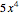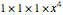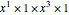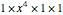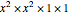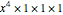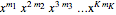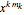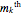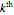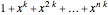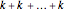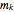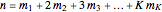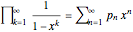The partition numbers 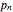 are 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, …. They count the number of ways of splitting an integer
are 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, …. They count the number of ways of splitting an integer  into a sum of positive integers, without regard to order. For instance,
into a sum of positive integers, without regard to order. For instance, 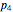 , the number of ways to partition 4, is 5 because there are 5 possible sums that add to 4: 4, 1+3, 2+2, 1+1+2, 1+1+1+1. By convention,
, the number of ways to partition 4, is 5 because there are 5 possible sums that add to 4: 4, 1+3, 2+2, 1+1+2, 1+1+1+1. By convention, 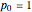 .
.
The left-hand side of the identity shows the product of geometric series 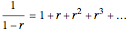 with common ratios
with common ratios 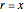 ,
, 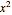 ,
, 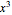 ,…,
,…, 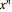 , each truncated to
, each truncated to  terms. The right-hand side multiplies them out and collects terms.
terms. The right-hand side multiplies them out and collects terms.
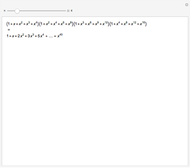
As an example, let  ; the term
; the term 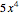 on the right is the sum of the five products
on the right is the sum of the five products 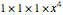 ,
, 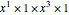 ,
, 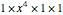 ,
, 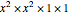 ,
, 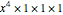 , where the factors in each product are in the order of the series they come from. These products correspond to the partitions 4, 1+3, 2+2, 1+1+2, 1+1+1+1.
, where the factors in each product are in the order of the series they come from. These products correspond to the partitions 4, 1+3, 2+2, 1+1+2, 1+1+1+1.
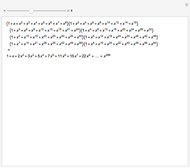
In general, an uncollected term in the expansion of the left side is of the form 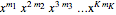 . The factor
. The factor 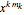 comes from the
comes from the 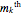 term of the
term of the 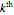 truncated series
truncated series 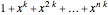 and contributes
and contributes 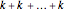 (
(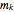 times) in the corresponding partition. Collecting terms amounts to counting the number of ways
times) in the corresponding partition. Collecting terms amounts to counting the number of ways 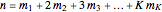 can be partitioned.
can be partitioned.
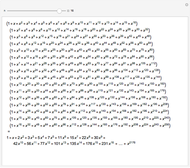
The generating function for 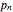 is thus
is thus 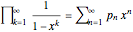 .
.
[less]

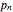 up to
up to  as the coefficients of
as the coefficients of 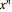 in the polynomial on the right.
in the polynomial on the right.