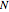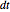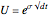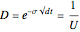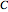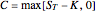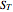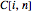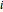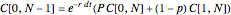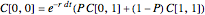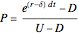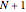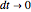European Binomial Option Pricing with Nonconstant Volatility

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
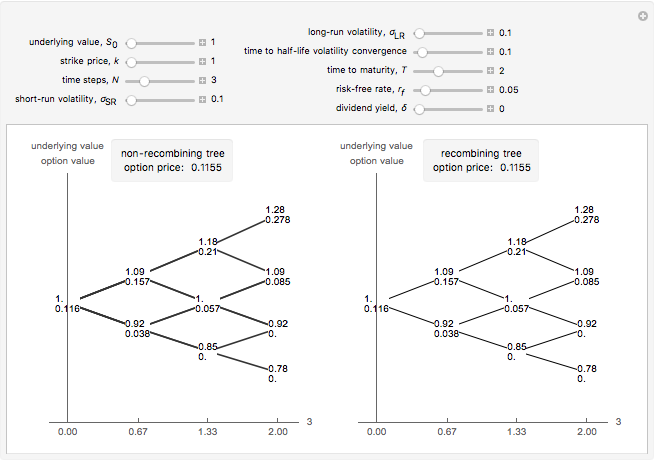
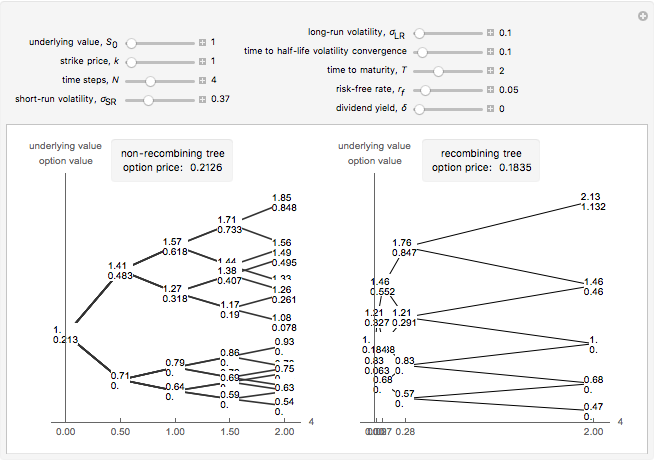
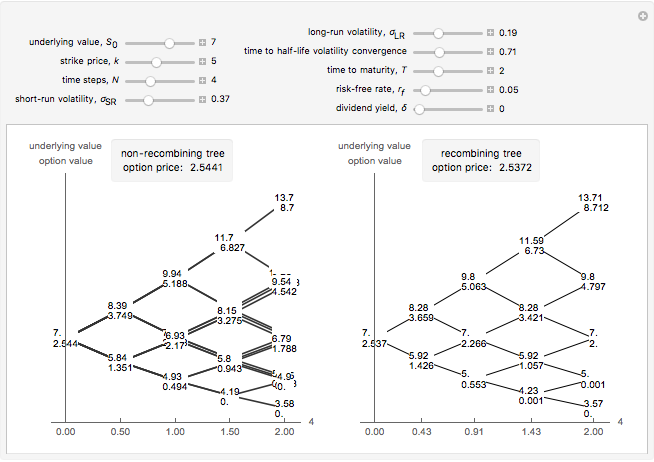
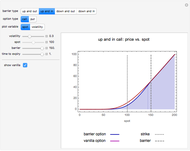
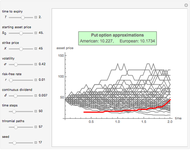
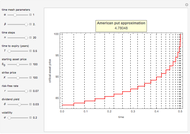
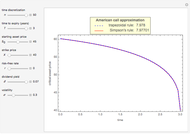
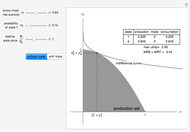
This Demonstration shows two approaches to using binomial option pricing for a European call option on an underlying asset with nonconstant volatility. The holder of the option has the right but not the obligation to purchase an asset at some fixed maturity date 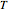 in the future for a price agreed upon today (known as the strike price
in the future for a price agreed upon today (known as the strike price  ).
).
Contributed by: Tom Stannard and Graeme Guthrie (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In [2], Guthrie presents a real options model where an investor is deciding whether or not to invest in a project. At time 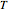 the option to invest expires. The investor begins with some level of uncertainty of the project's true value
the option to invest expires. The investor begins with some level of uncertainty of the project's true value  . Each period the investor receives a signal
. Each period the investor receives a signal 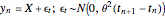 and uses this signal to update their perception of the investment's true value
and uses this signal to update their perception of the investment's true value 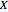 from
from 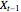 to
to 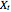 ;
;  is a constant that determines the amount of noise in each signal. High
is a constant that determines the amount of noise in each signal. High  means each signal is noisy and the investor cannot update their perception very much (
means each signal is noisy and the investor cannot update their perception very much ( and
and  are inversely related). The initial uncertainty of the true value is
are inversely related). The initial uncertainty of the true value is 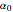 , and after each signal this is also updated and decreased to
, and after each signal this is also updated and decreased to 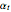 to reflect that more information about the project has been revealed;
to reflect that more information about the project has been revealed;  is the volatility of the market (that will become the long-term volatility). The volatility at each time step
is the volatility of the market (that will become the long-term volatility). The volatility at each time step 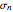 for this learning process is
for this learning process is
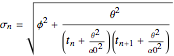 .
.
If we use this for constant-sized time steps (constant 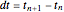 ), then we get the non-recombining case. This is because the noise term and the residual uncertainty make the volatility decrease over time. That is, early information is more revealing than later information about the project's true value. [2] presents an alternative approach where constant movements can be calculated by
), then we get the non-recombining case. This is because the noise term and the residual uncertainty make the volatility decrease over time. That is, early information is more revealing than later information about the project's true value. [2] presents an alternative approach where constant movements can be calculated by
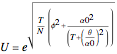
subject to time steps calculated using
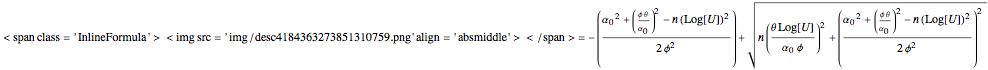 .
.
In order to apply this to an option on an asset, we can replace the initial uncertainty  with a share price at the inception of the contract
with a share price at the inception of the contract 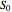 . We then specify
. We then specify  as the long-term volatility of the asset and calculate short- and long-run volatility along with the time to half-life convergence of the two to calculate
as the long-term volatility of the asset and calculate short- and long-run volatility along with the time to half-life convergence of the two to calculate  and
and 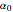 as
as
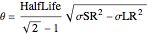 ,
,
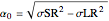 .
.
These values can then be placed into the equations for  ,
, 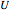 , and
, and 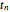 , and the models in the Demonstration can be built.
, and the models in the Demonstration can be built.
References
[1] J. Cox, S. Ross, M. Rubinstein, "Option Pricing: A Simplified Approach," Journal of Financial Economics, 7(3), 1979 pp. 229–263. doi:10.1016/0304-405X(79)90015-1.
[2] G. Guthrie, "Learning Options and Binomial Trees," Wilmott Journal: The International Journal of Innovative Quantitative Finance Research, 3(1), 2011 pp. 1–23. doi:10.1002/wilj.42.
[3] J. C. Hull, Options, Futures, and Other Derivatives, 8th ed., Boston: Prentice Hall, 2012.
Permanent Citation