Evolution of Monomer Sequence Distribution in Polymer Analogous Reaction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
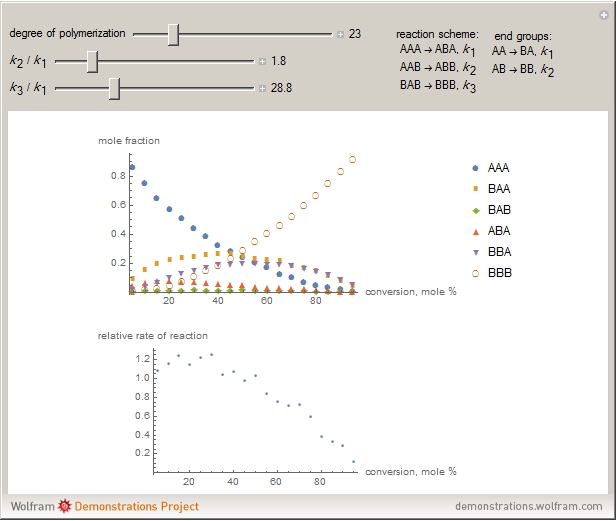
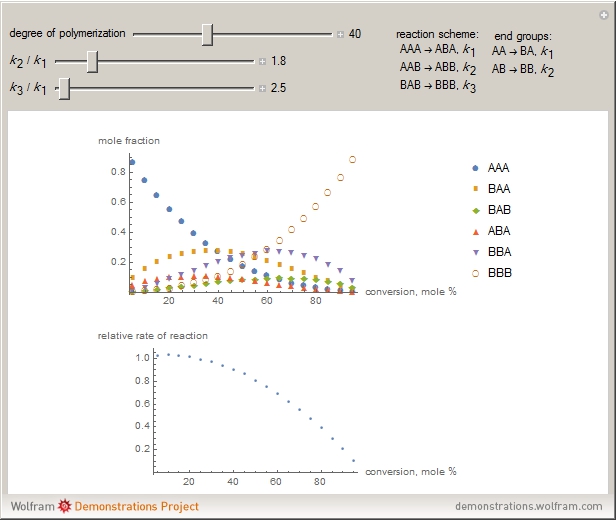
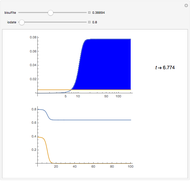
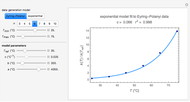
This Demonstration shows the rate constant ratio effect in a polymer analogous reaction. The first-order effect of neighboring groups is taken into account. Also considered is the effect of an external reagent for homopolymers or homooligomers on the monomer sequence distribution and the relative reaction rate as a function of functional group conversion. Relative rate means the ratio of the rate at a given conversion to the initial rate provided that all rate-determining concentrations of external reagents are constant.
Contributed by: A. A. Koledenkov (January 2019)
Open content licensed under CC BY-NC-SA
Details
The rate of polymer analogous reactions generally depends on the nearest to the reactive functional group. If only neighboring groups have a significant effect on reaction rate, then this phenomenon is called a first-order neighbor effect. In this case, for a complete description of the kinetics of the process, it is necessary to consider the triads of monomeric units:
 ,
,  ,
,
 ,
,  ,
,
 ,
, ,
,
where  is the pseudo-first-order reaction rate constant.
is the pseudo-first-order reaction rate constant.
For end groups, accept:
 ,
,  ,
,
 ,
,  .
.
The total rate of polymer analogous reaction is
 .
.
The complexity of integrating this equation lies in the complicated dependence of the molar fractions of individual sequences. Monte Carlo simulation is an alternative way to solve this problem.
This Demonstration lets you simulate the evolution of monomer sequence distribution during polymer analogous reaction with the second reagent in the solution. A change in the concentration of the reagent in the solution does not affect the evolution of the distribution provided that there is no specific interaction with the functional groups of the polymer.
Snapshots
Permanent Citation