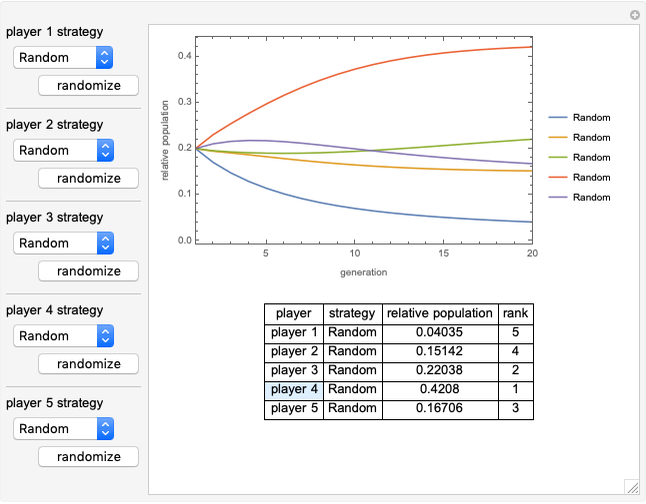
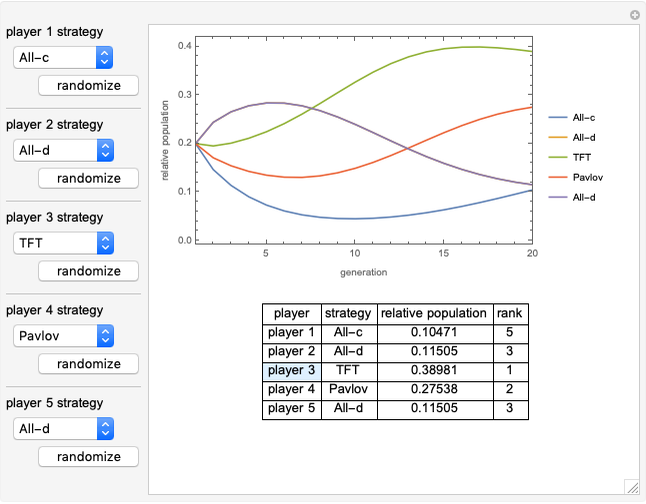
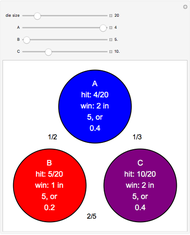
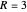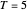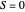Evolutionary Prisoner's Dilemma Tournaments

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
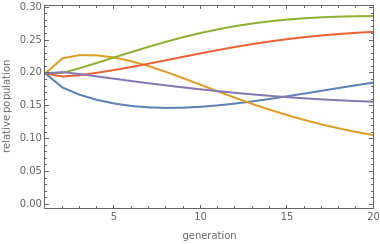
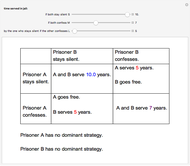
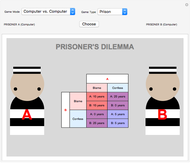
The prisoner's dilemma is a two-player game in which each player (prisoner) can either "cooperate" (stay silent) or "defect" (betray the other prisoner). If both players cooperate, they each get a reward 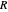 ; if both defect, they get a punishment payoff
; if both defect, they get a punishment payoff 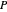 ; if one player defects and the other cooperates, the defecting player gets a temptation payoff
; if one player defects and the other cooperates, the defecting player gets a temptation payoff 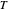 , while the cooperating player receives a sucker payoff
, while the cooperating player receives a sucker payoff 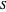 . In the standard form of the game,
. In the standard form of the game,
Contributed by: Jiusi Li (April 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
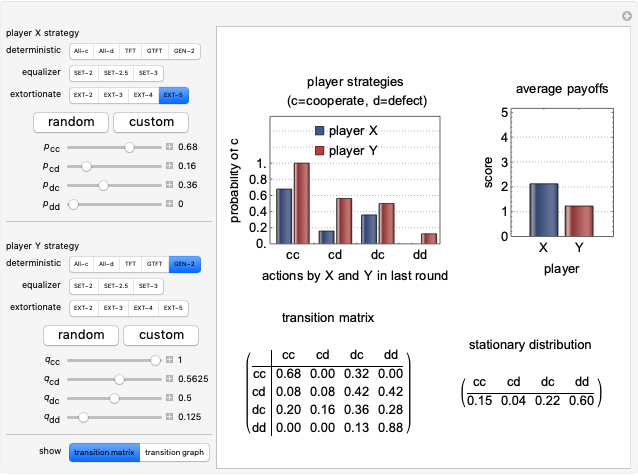
All of the strategies implemented in this Demonstration are "memory-one" strategies; that is, the action of a player in a given round depends only on the actions by the two players in the previous round. Memory-one strategies can be described by a strategy vector 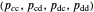 whose components represent the probabilities that the player cooperates given a particular pair of actions by the two players in the previous round. For example, in a strategy with vector
whose components represent the probabilities that the player cooperates given a particular pair of actions by the two players in the previous round. For example, in a strategy with vector 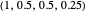 the player always cooperates if both players cooperated in the previous round, cooperates with 50% probability if one player cooperated and the other player defected in the previous round, and cooperates with 25% probability if both players defected in the previous round.
the player always cooperates if both players cooperated in the previous round, cooperates with 50% probability if one player cooperated and the other player defected in the previous round, and cooperates with 25% probability if both players defected in the previous round.
Memory-one strategies can be modeled by a Markov chain on the four states CC, CD, DC, DD, and the stationary distribution of this Markov chain determines the average payoffs for the two players over a large number of games [2, 4]. The stationary distribution is an eigenvector with eigenvalue 1 of the transition matrix of the Markov chain.
Controls
All-c: the player always cooperates. Strategy vector 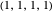 .
.
All-d: the player always defects. Strategy vector  .
.
TFT (tit for tat [1]): the player cooperates if the opponent cooperated in the previous round, and defects if the opponent defected in the previous round. Strategy vector 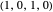 .
.
GTFT (generous tit for tat [3]): the player cooperates after every instance of the opponent’s cooperations and after 25% of the opponent’s defections. Strategy vector 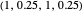 .
.
SET-2 (an example of an equalizer strategy [3, 4]): this strategy forces the opponent’s payoff to be 2 regardless of what strategy the opponent uses. Strategy vector: 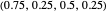 .
.
EXTORT-2 (an example of an extortionate strategy [3, 4]): a strategy that guarantees the player a higher or equal payoff no matter what the opponent plays. Strategy vector: 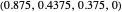 .
.
GEN-2 (generous zero-determinant strategy [3]): strategy vector 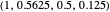 .
.
Spiteful [3]: the player cooperates if both players cooperated in the previous round and defects otherwise. Strategy vector 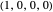 .
.
Pavlov [3]: the player cooperates if both players made the same decision in the previous move, and defects otherwise. Strategy vector 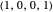 .
.
Random: a random strategy, given by a vector whose components are random numbers in  .
.
References
[1] R. M. Axelrod, The Evolution of Cooperation, New York: Basic Books, 1984.
[2] S. Kuhn. "Prisoner's Dilemma." The Stanford Encyclopedia of Philosophy. (Apr 14, 2020) plato.stanford.edu/entries/prisoner-dilemma.
[3] P. Mathieu and J.-P. Delahaye, "New Winning Strategies for the Iterated Prisoner's Dilemma," Journal of Artificial Societies and Social Simulation, 20(4), 2017 pp. 1–12. doi:10.18564/jasss.3517.
[4] W. H. Press and F. J. Dyson, "Iterated Prisoner’s Dilemma Contains Strategies That Dominate Any Evolutionary Opponent," Proceedings of the National Academy of Sciences, 109(26), 2012 pp. 10409–10413. doi:10.1073/pnas.1206569109.
Permanent Citation