Filling a Container Defined by a Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
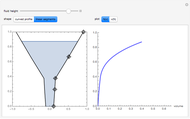
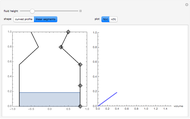
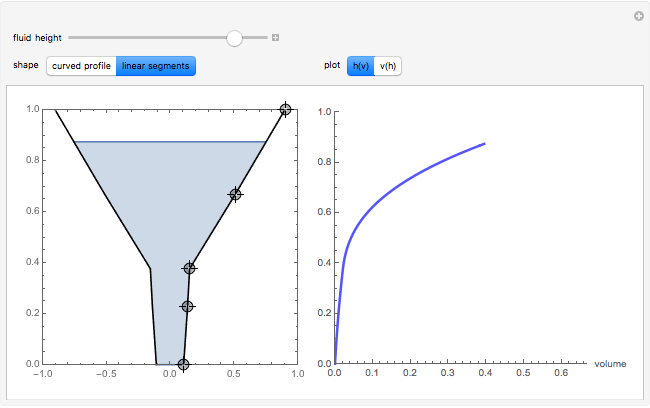
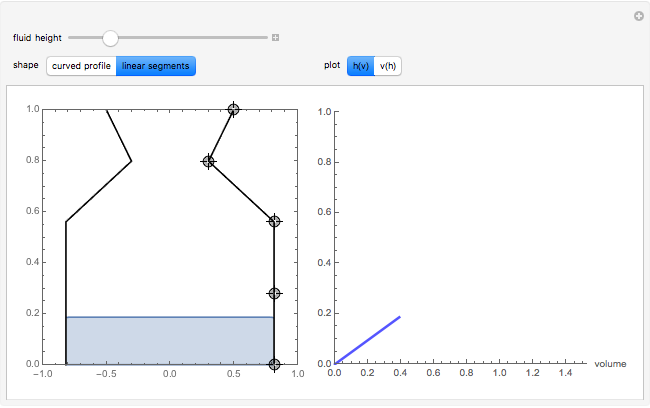
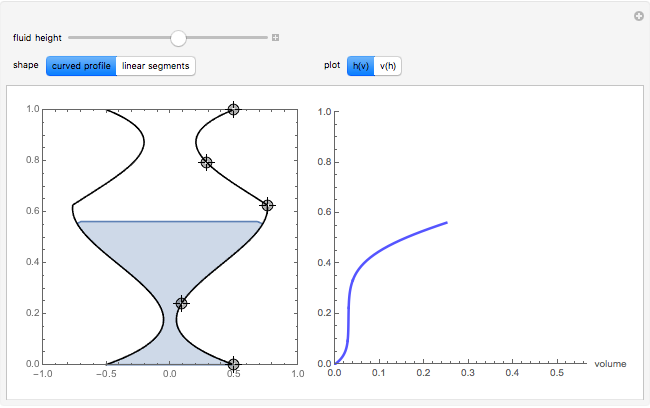
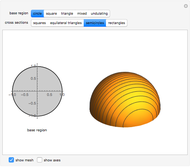
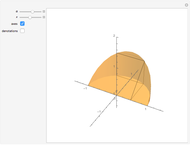
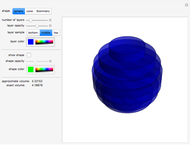
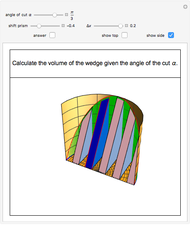
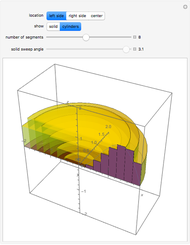
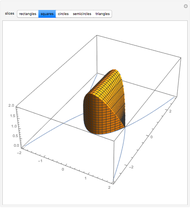
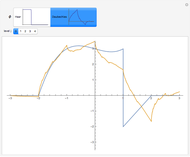
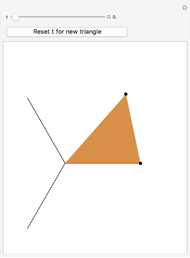
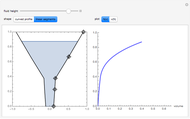
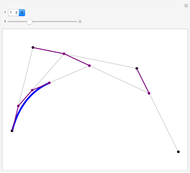
The graphic on the left shows the profile of a circularly symmetric container centered on the vertical axis. Its shape is controlled by moving the locators and selecting either a curved profile or linear segments joining the locators. As you move the slider, the height of the fluid changes. The graph on the right shows either fluid height as a function of volume or fluid volume as a function of height.
Contributed by: Bruce Atwood (Beloit College) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Teaching suggestions: As a precalculus exercise, before moving the slider to the right, try to sketch  for a particular container shape. First try this with simple containers whose profiles are linear segments and then try curved profiles. For a calculus exercise, indicate on the sketch where the curves are concave up, concave down, or neither. Where are the inflection point(s), if any? What is the relationship between
for a particular container shape. First try this with simple containers whose profiles are linear segments and then try curved profiles. For a calculus exercise, indicate on the sketch where the curves are concave up, concave down, or neither. Where are the inflection point(s), if any? What is the relationship between  and
and  ? Students might find it easier to sketch
? Students might find it easier to sketch  if they think of pouring a liquid into the container at a constant rate and then considering
if they think of pouring a liquid into the container at a constant rate and then considering  .
.
Permanent Citation
"Filling a Container Defined by a Curve"
http://demonstrations.wolfram.com/FillingAContainerDefinedByACurve/
Wolfram Demonstrations Project
Published: March 7 2011