Filling a Square with Random Disks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
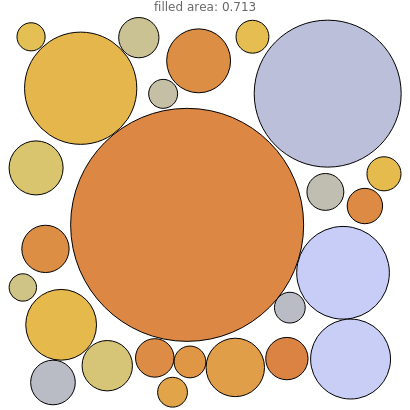
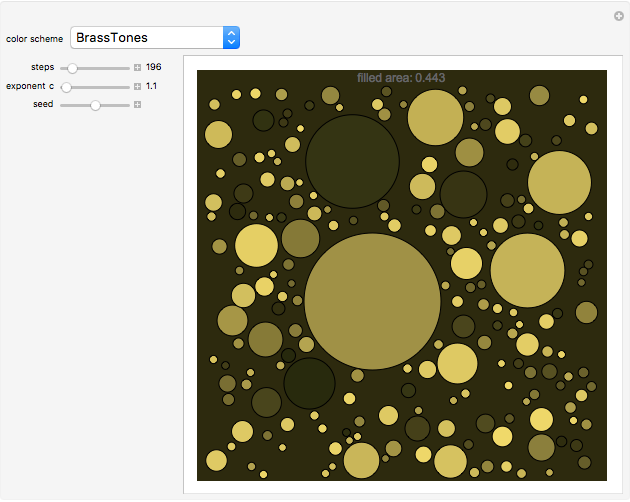
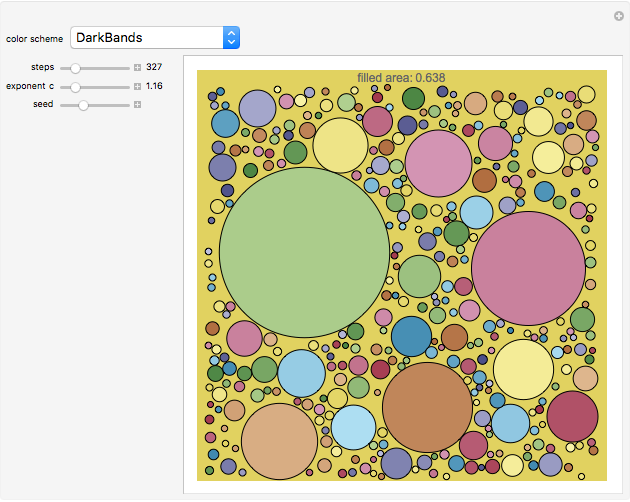
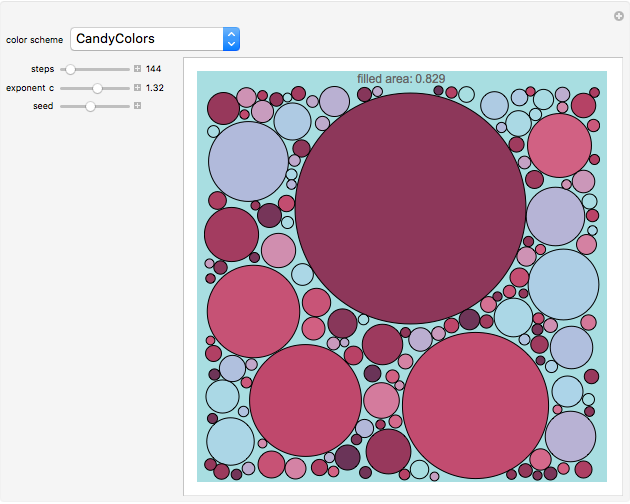
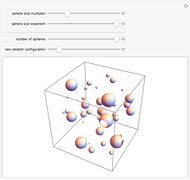
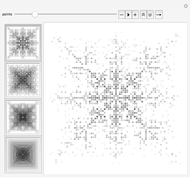
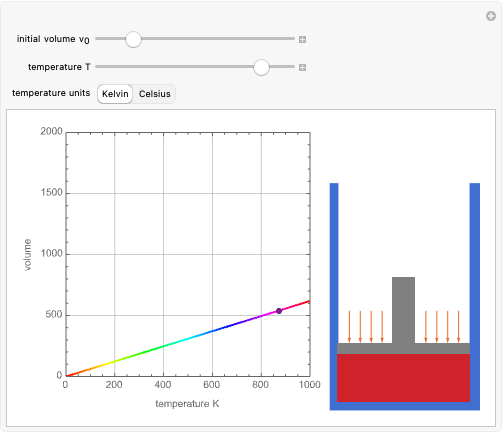
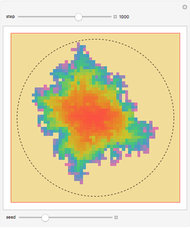
A unit square is filled randomly with non-overlapping circles of decreasing radius according to a power law; the resulting set has fractal properties.
Contributed by: Enrique Zeleny (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The area of each circle decreases as  , where
, where  is an integer and
is an integer and  is an exponent between 1.1 and 1.5, which ensures convergence and interesting pictures. In fact, summing all areas gives the Riemann zeta function, with a starting area for the first circle
is an exponent between 1.1 and 1.5, which ensures convergence and interesting pictures. In fact, summing all areas gives the Riemann zeta function, with a starting area for the first circle  satisfying the relation
satisfying the relation
 .
.
For a high number of steps and values of  near 1.5, the number of iterations required grows; in that case the number of iterations is limited to one million.
near 1.5, the number of iterations required grows; in that case the number of iterations is limited to one million.
For a variety of designs, extensions to 3D, and estimates of fractal dimensions, visit Paul Bourke's web page.
Permanent Citation