Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Finding Comparative Advantage

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

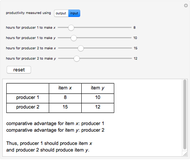
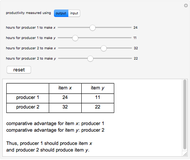
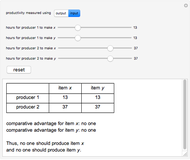
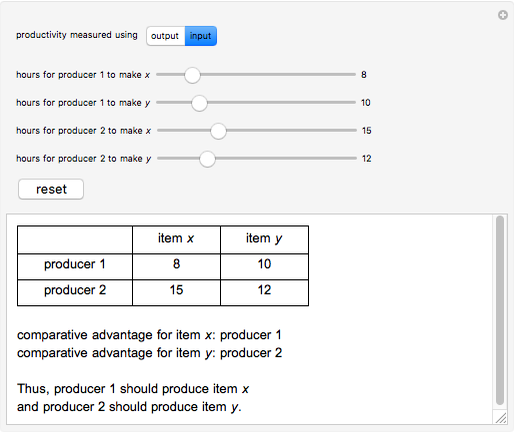
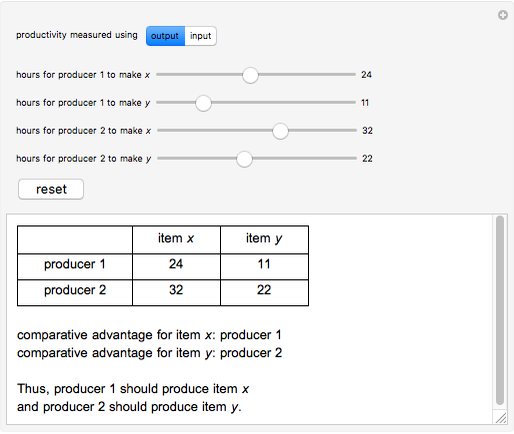
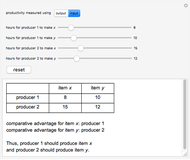
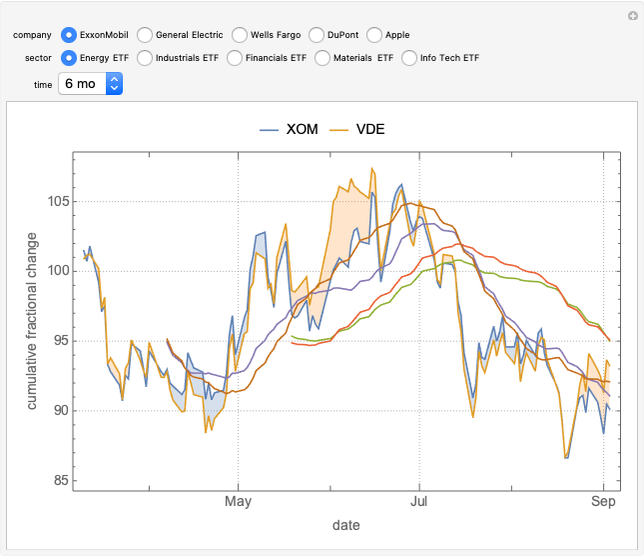
Two producers make two products. This Demonstration calculates which producer has the comparative advantage in making a particular product. Comparative advantage shows which producer is more efficient in its production of a certain item and is found by discerning which party has a lower opportunity cost, which is dependent on the ratio of output/input. This analysis is used in the high-school level study of economics to determine which producer should specialize in making a specific product; this example, however, has its limitations: it only considers two producers and two products.

[more]

You can choose whether the productivity is determined by the output of final products or by the input, which might be raw materials or capital. The numbers given are the number of hours required by each producer to produce one unit of either item or item .

[less]

Contributed by: Kathy Wang, YeRin You and Michael Kelly (April 2018)
Open content licensed under CC BY-NC-SA

Snapshots

Details

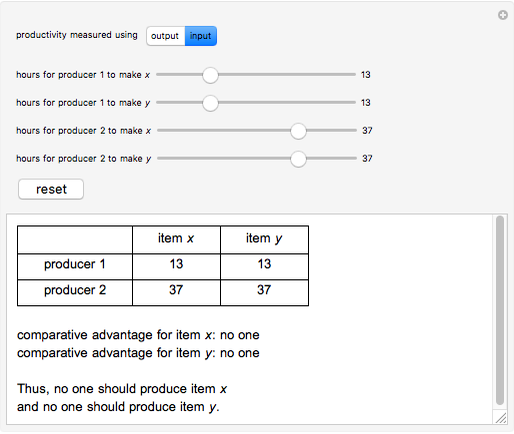
Use this Demonstration to calculate comparative advantage in two different situations: input and output. Input is the amount of resources producers use to make an item. Less input of resources results in a greater comparative advantage. Output is the number of items a producer can make. More output means a greater comparative advantage. Switching from input to output (or vice versa) inverts the comparative advantage, as in an output question, producers desire to make more products, but in an input question, producers desire to use less resources.

The decision rule depends upon comparing ratios of hours by each producer to produce the different items, that is, by comparing . This leads to symmetrical results, so that

.

Reference

[1] C. R. McConnell and S. L. Brue, Macroeconomics: Principles, Problems, and Policies, 17th ed., Boston, MA: McGraw-Hill/Irwin, 2008.

This was a project for Advanced Topics in Mathematics II, 2017–2018, Torrey Pines High School, San Diego, CA.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send