Finding the Area of a 3D Surface with Parallelograms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
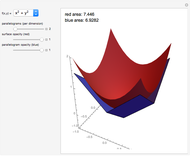
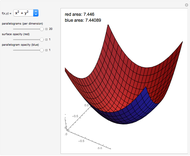
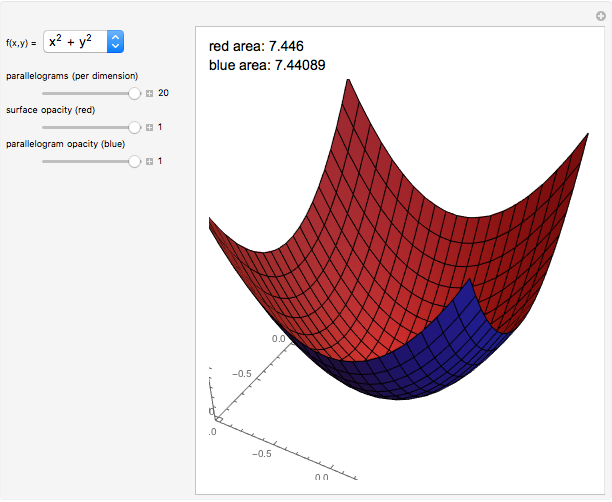
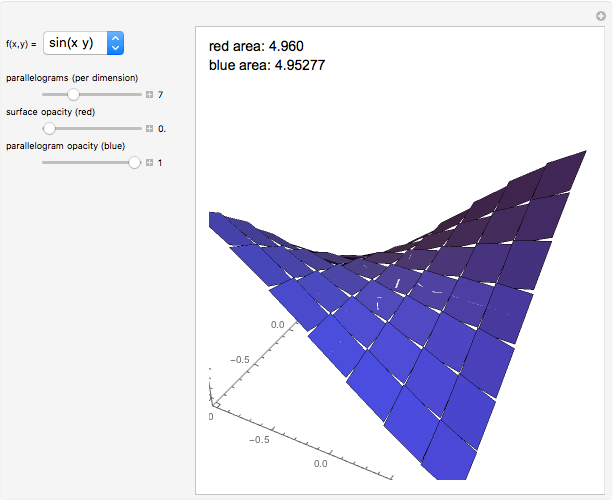
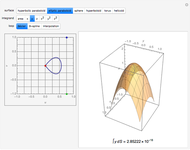
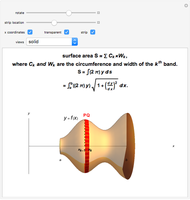
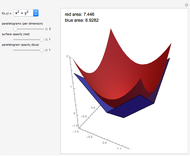
This Demonstration shows a sequence of Riemann-like approximations of the area of a surface in three-space. The area of a surface can be approximated by using an array of parallelograms that are tangent to the surface at their centers. The magnitude of the cross product of two vectors that describe adjacent sides of a parallelogram yields the area of the parallelogram, and finding the sum of all of these areas results in a good approximation of the area of the surface. As the number of parallelograms increases, the approximation becomes more accurate, as you can see by using the slider. The double integral is constructed using the same idea of summing approximations taken over successively smaller regions of the  plane.
plane.
Contributed by: Mark Peterson (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
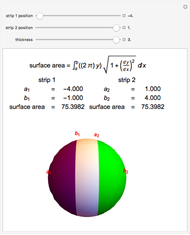
The surface area of a function 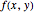 over the square
over the square  and
and  is given by the expression
is given by the expression 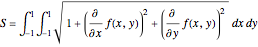 . The total surface area of all of the parallelograms over the same intervals is given by the expression
. The total surface area of all of the parallelograms over the same intervals is given by the expression  . Note that these expressions are essentially identical when
. Note that these expressions are essentially identical when  (the number of divisions per dimension) approaches infinity.
(the number of divisions per dimension) approaches infinity.
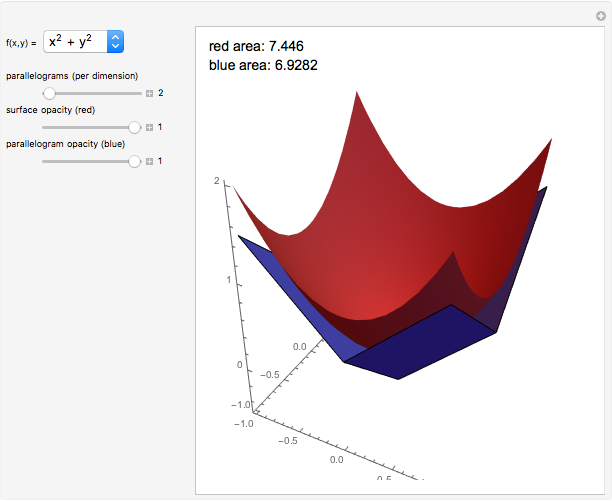
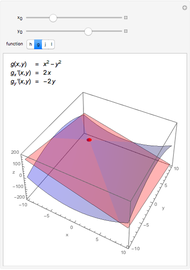
Snapshot 1: With only a few parallelograms, the approximation is very rough. The blue parallelograms only loosely fit the red surface, and there is a significant difference between the surface areas.
Snapshot 2: As the number of iterations is increased, the approximation becomes much better. Here the blue parallelograms look nearly identical to the red surface, and the surface areas are almost the same.
Snapshot 3: The edges of adjacent parallelograms are not necessarily parallel. In other words, the array of parallelograms does not always create a continuous surface.
Permanent Citation