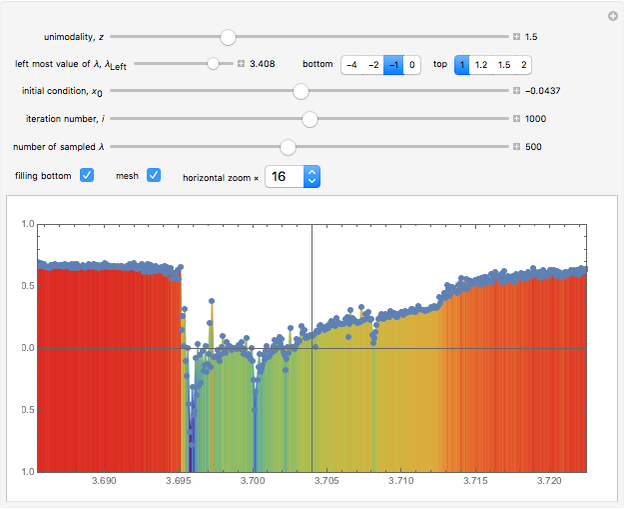
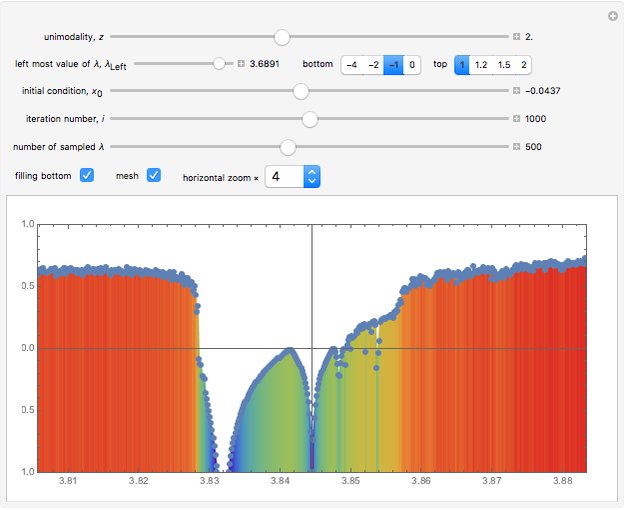
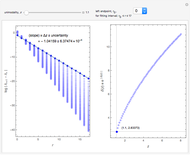
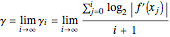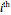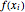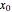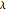Finite Lyapunov Exponent for Generalized Logistic Maps with z-Unimodality

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
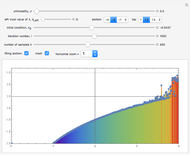
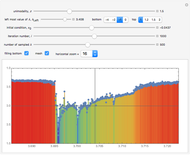
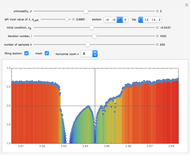
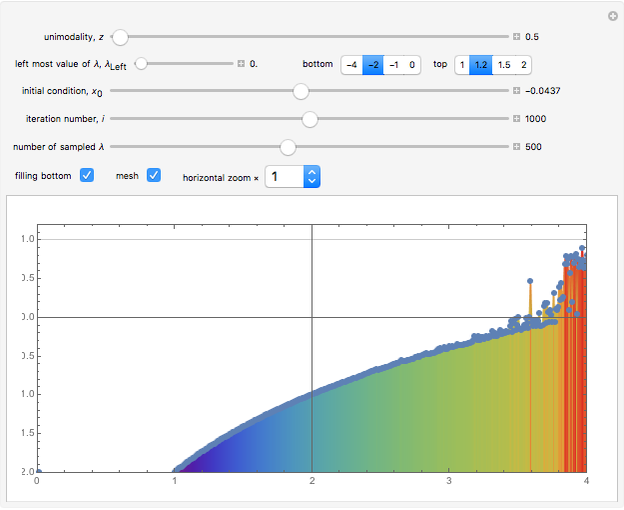
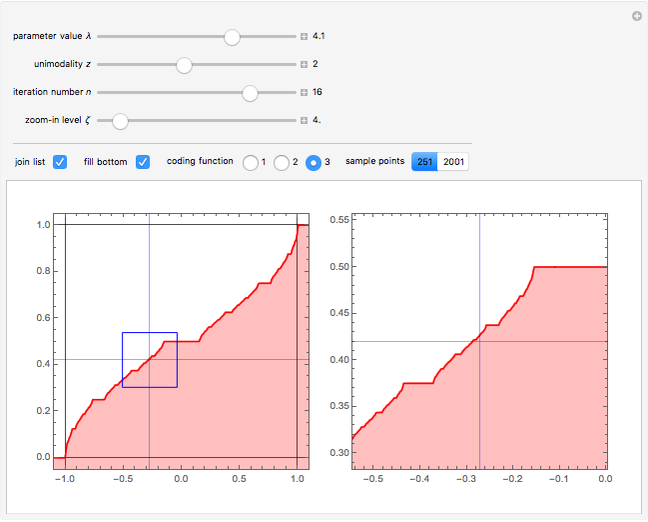
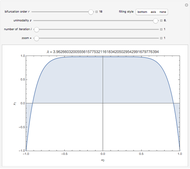
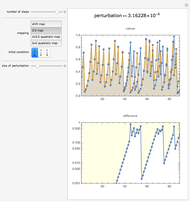
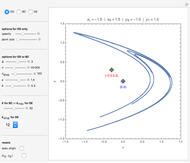
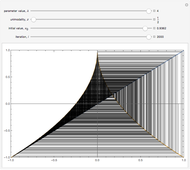
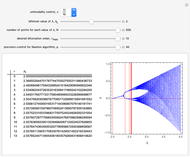
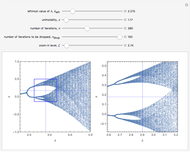
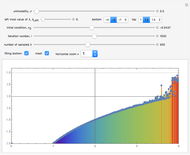
This Demonstration shows a finite Lyapunov exponent 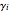 of a one-dimensional unimodal map
of a one-dimensional unimodal map 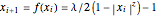 , which is a generalization of the well-known logistic map
, which is a generalization of the well-known logistic map 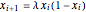 . The related Lyapunov exponent
. The related Lyapunov exponent  can be defined by
can be defined by
Contributed by: Ki-Jung Moon (January 2014)
Based on a program by: Stephen Wolfram
Open content licensed under CC BY-NC-SA
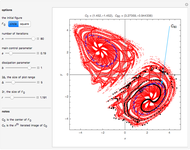
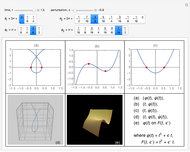
Snapshots
Details
References
[1] S. H. Strogatz, Nonlinear Dynamics and Chaos, New York: Perseus Books Publishing, 1994.
[2] K. T. Alligood, T. D. Sauer, and J. A. Yorke, Chaos: An Introduction to Dynamical Systems, New York: Springer, 1996.
[3] H.-O. Peitgen, H. Jürgens, and D. Saupe, Chaos and Fractals: New Frontiers of Science, 2nd ed., New York: Springer, 2004.
[4] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media, 2002.
[5] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.
[6] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.
[7] K.-J. Moon, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 18, 2008 pp. 023104.
[8] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 20, 2010 pp. 049902.
Permanent Citation