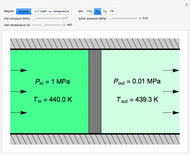
First- and Second-Order Transfer Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
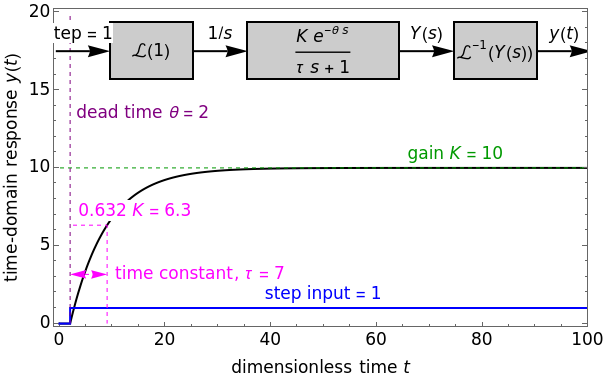
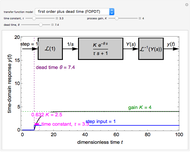
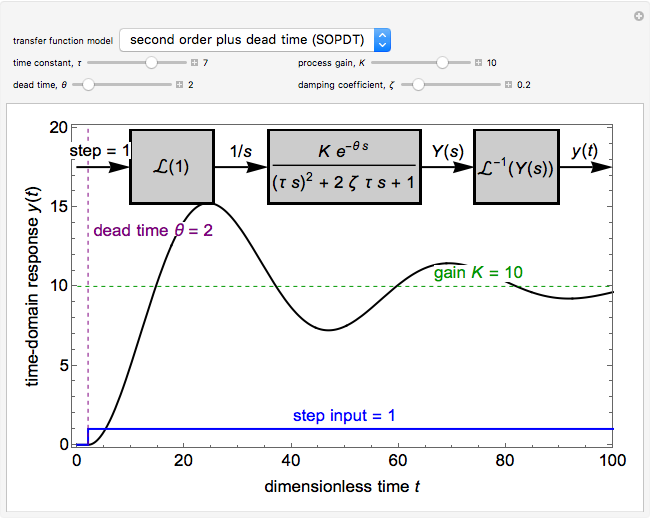
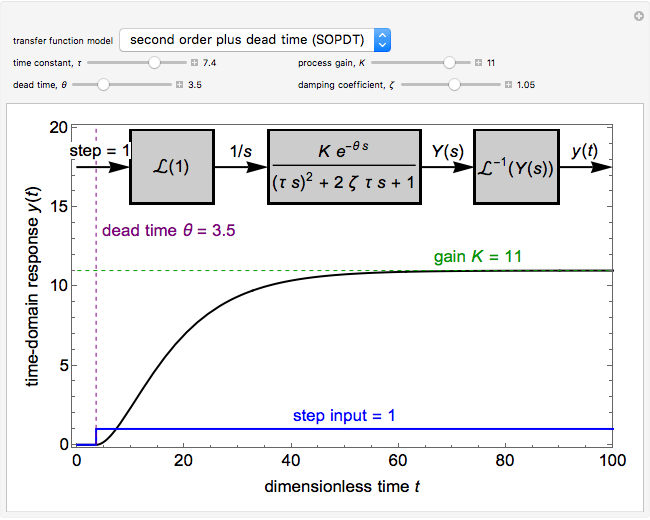
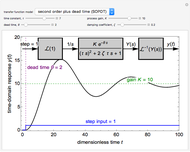
This Demonstration plots the time-domain response of a system with a step input of unity. Select either a first-order plus dead time (FOPDT) model or a second-order plus dead time (SOPDT) model. Set the time constant 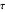 to change how quickly the system reaches a new steady state, the process gain
to change how quickly the system reaches a new steady state, the process gain 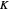 to change how aggressively the system responds to the unity step input and the dead time
to change how aggressively the system responds to the unity step input and the dead time  that delays the system response by a value of
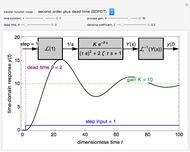
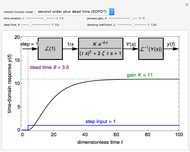
that delays the system response by a value of  . For the second-order process, change the damping coefficient
. For the second-order process, change the damping coefficient  with a slider. The damping coefficient is a measure of the magnitude of damping, which affects the degree of oscillation in the response. Dimensionless time is used.
with a slider. The damping coefficient is a measure of the magnitude of damping, which affects the degree of oscillation in the response. Dimensionless time is used.
Contributed by: Rachael L. Baumann and Adam J. Johnston (September 2017)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The general first-order transfer function in the Laplace domain is:
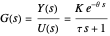 ,
,
where 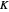 is the process gain,
is the process gain, 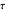 is the time constant,
is the time constant,  is the system dead time or lag and
is the system dead time or lag and  is a Laplace variable. The process gain is the ratio of the output response to the input (unit step for this Demonstration), the time constant determines how quickly the process responds or how rapidly the output changes and the dead time delays the system response by the amount
is a Laplace variable. The process gain is the ratio of the output response to the input (unit step for this Demonstration), the time constant determines how quickly the process responds or how rapidly the output changes and the dead time delays the system response by the amount  .
.
This Demonstration converts from the Laplace domain to the time domain for a step-response input. For a first-order transfer function, the time-domain response is:
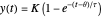 .
.
The general second-order transfer function in the Laplace domain is:
 ,
,
where  is the (dimensionless) damping coefficient.
is the (dimensionless) damping coefficient.
For a step-response input, the time-domain response for various damping coefficients are:
Overdamped (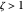 ):
):
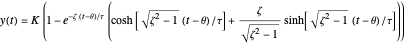 .
.
Critically damped (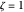 ):
):
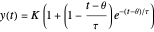 .
.
Underdamped ( ):
):
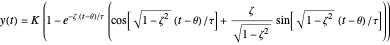 .
.
Reference
[1] D. E. Seborg, D. A. Mellichamp, T. F. Edgar and F. J. Doyle, III, Process Dynamics and Control, 3rd ed., Hoboken: John Wiley & Sons, 2011 pp. 76, 81.
Permanent Citation