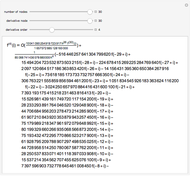
Fit, Interpolation, or Polynomial Interpolation in Uncertain Calculus

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
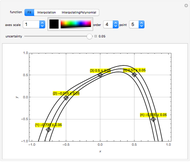
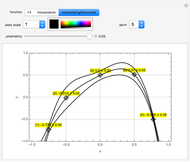
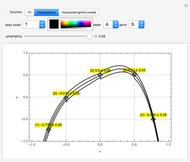
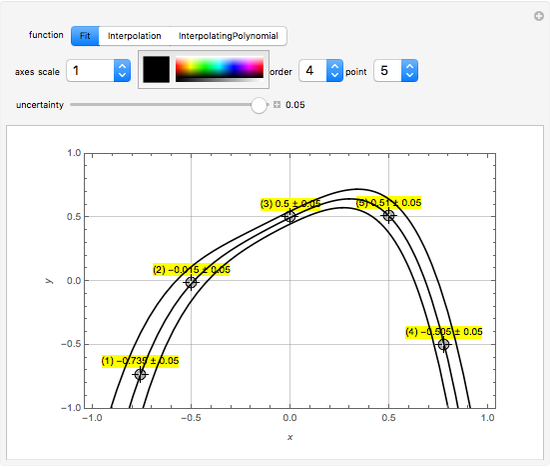
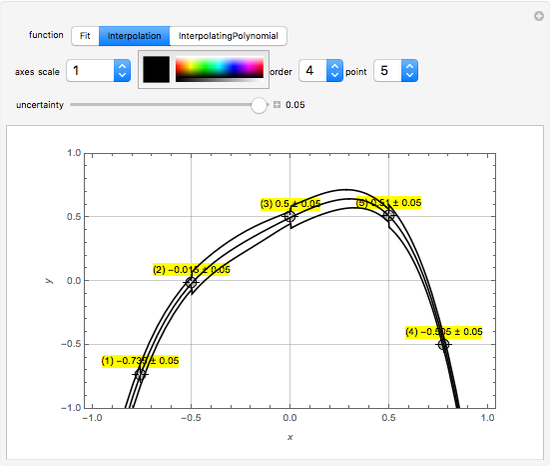
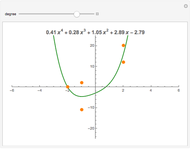
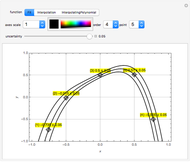
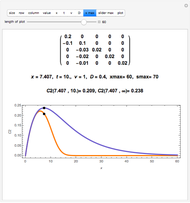
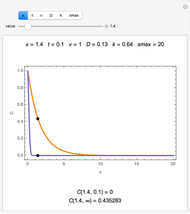
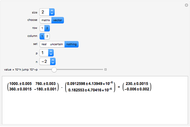
Initially there is one locator, representing a point in a region defined by the popup menu "axes scale". Each point is labeled  , where
, where  is the current number of the locator,
is the current number of the locator,  is its vertical coordinate, and
is its vertical coordinate, and  is the uncertainty of
is the uncertainty of  as set by the slider. The popup menu "point" connects a point
as set by the slider. The popup menu "point" connects a point  to the "uncertainty" slider. Deleting locators reorders the numbers and the "point" number jumps to zero, which means the slider is not connected to any point.
to the "uncertainty" slider. Deleting locators reorders the numbers and the "point" number jumps to zero, which means the slider is not connected to any point.
Contributed by: Valter Yoshihiko Aibe and Mikhail Dimitrov Mikhailov, INMETRO, Brazil (July 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The rules given in the initialization section are borrowed from the Uncertain Calculus, introduced in [1].
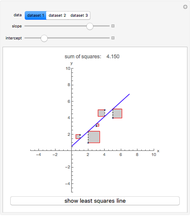
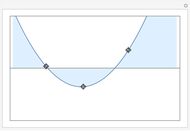
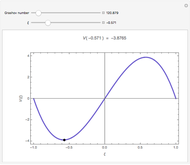
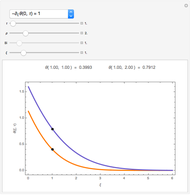
The Demonstration combines Demonstrations [2] to [5], interpolating  and extending them to work with uncertain numbers for
and extending them to work with uncertain numbers for  , explored also in [6] and [7].
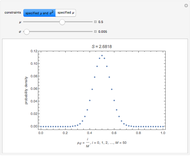
In general, both
, explored also in [6] and [7].
In general, both  and
and  in a measured function are uncertain numbers
in a measured function are uncertain numbers  and
and  , but here it is assumed that
, but here it is assumed that 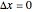 . This assumption is based on the possibility to transfer the uncertainty
. This assumption is based on the possibility to transfer the uncertainty 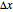 to the enlarged uncertain
to the enlarged uncertain  of the uncertain number
of the uncertain number 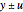 , where
, where  [8, p. 125]. Here
[8, p. 125]. Here 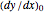 is an estimated value of the derivative
is an estimated value of the derivative  that could be obtained by successive approximations.
that could be obtained by successive approximations.
References:
[1] V. Y. Aibe and M. D. Mikhailov, "Uncertainty Calculus in Metrology," Proceedings of ENCIT 2008, 12th Brazilian Congress of Thermal Engineering and Sciences, Belo Horizonte, MG, Brazil, November 10–14, 2008.
[3] Interpolating a Set of Data
[4] Fitting a Curve to Five Points
[5] Curve Fitting
[6] Solving Matrix Systems with Real, Interval, or Uncertain Elements
[7] Area, Perimeter, and Diagonal of a Rectangle with Uncertain Sides
[8] José Henrique Vuolo, Fundamentos da Teoria de Erros, 2nd ed., 2nd printing, Sao Paulo, Brazil: Edgar Blucher, LTDA, 2000.
Permanent Citation