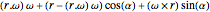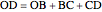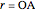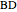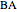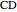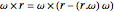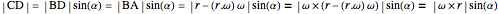Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Formula for 3D Rotation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

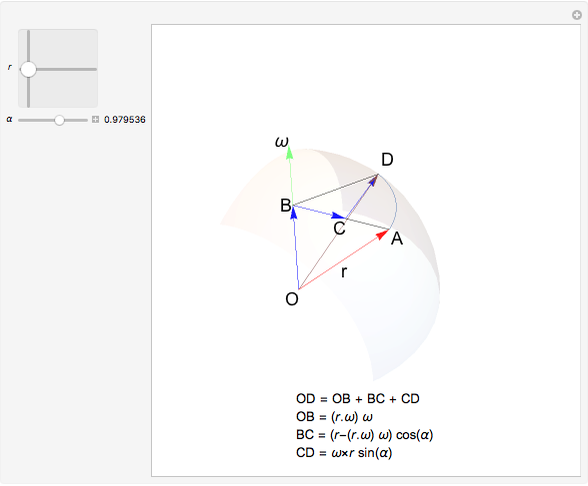
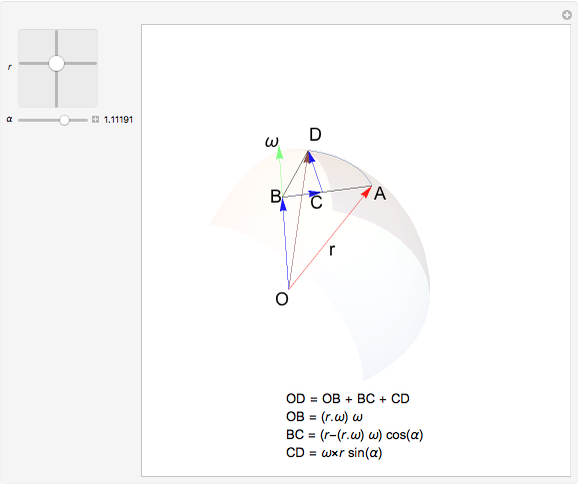
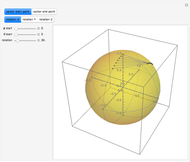
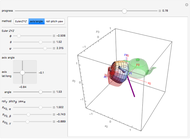
This Demonstration explains a formula for the rotation of the vector around the axis given by the unit vector through the angle .

[more]

The formula is , using the dot and cross product of vectors.

The resultant vector is .

The vector is the orthogonal projection of the vector onto the vector .

The vector is the result of the rotation of the vector around through the angle .

The vector is the orthogonal projection of onto .

is the orthogonal projection of onto .

[less]

Contributed by: Izidor Hafner (September 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send