Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

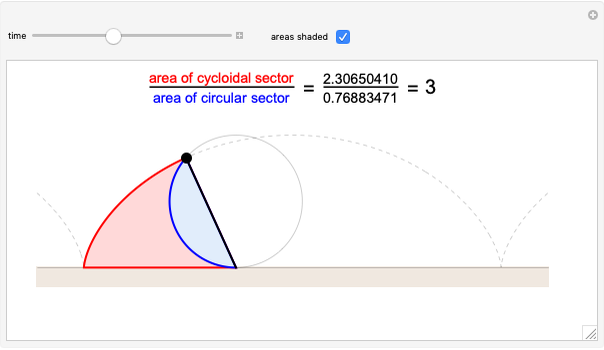
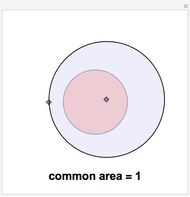
Fraction of a Circle Covered by Arcs of a Given Length

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

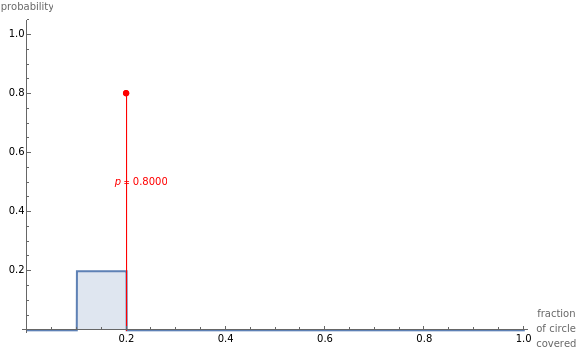
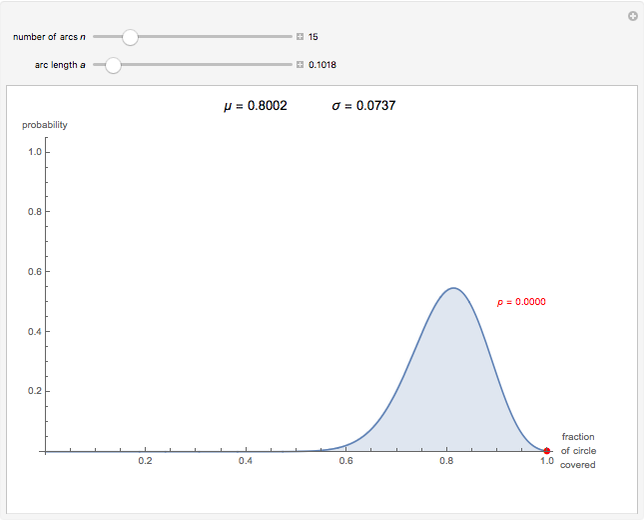
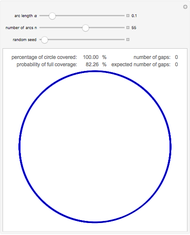
This Demonstration shows the probability density function for the fraction of a circle with unit circumference covered by random arcs, each of length . This probability distribution is a mixed distribution. The discrete probability mass 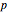is shown and captioned in red, and the continuous probability density is shown in blue (scaled by ). and are the mean and variance of the fraction covered.

Contributed by: Aaron Becker (March 2011)
Open content licensed under CC BY-NC-SA

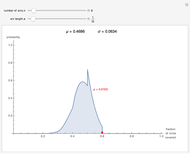
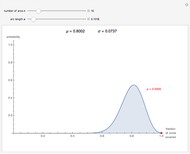
Snapshots

Details

The probability density function is continuous between 0 and , where is the minimum of 1 and 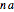, and has a discrete probability at . For 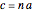, the discrete part 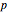is the probability that all arcs do not overlap. When , the discrete part 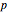is the probability of complete coverage of the circle. The probability density function and probability mass functions shown are calculated in [1].

Reference

[1] H. Solomon, Geometric Probability, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1978 pp. 75–96.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send