Fraunhofer Diffraction Using a Fast Fourier Transform

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
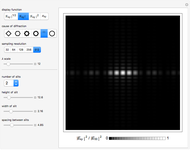
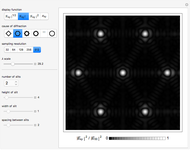
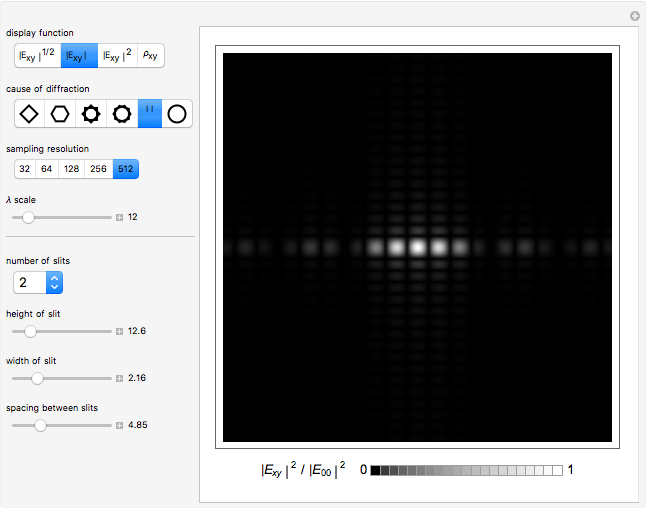
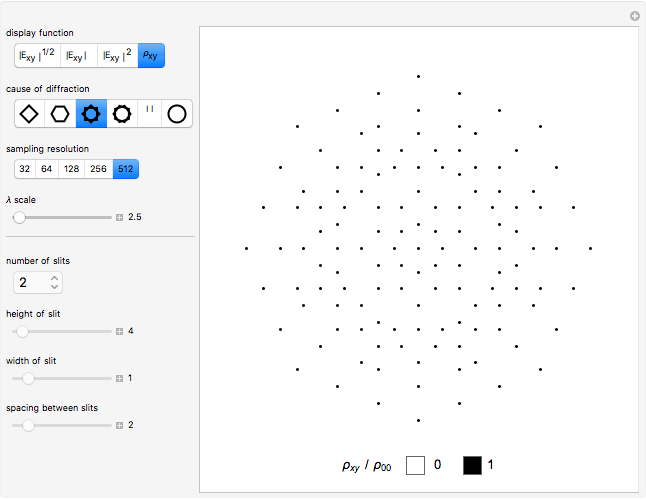
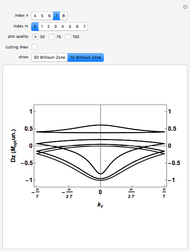
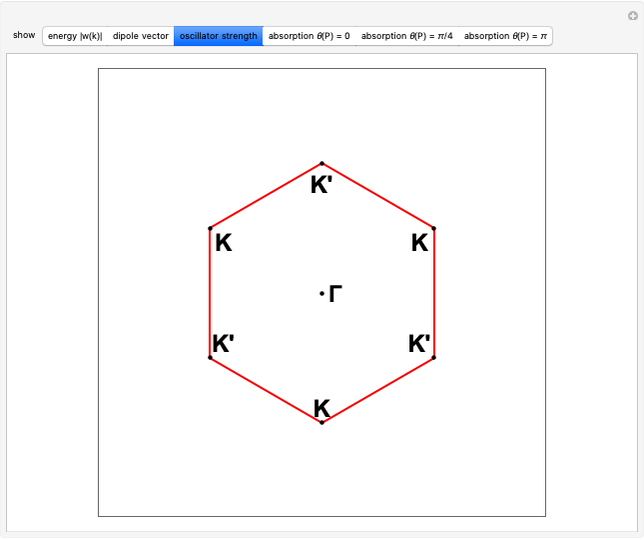
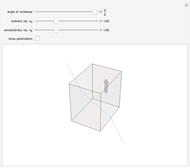
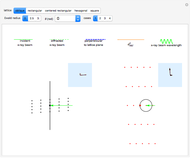
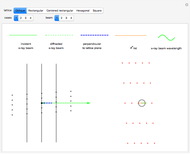
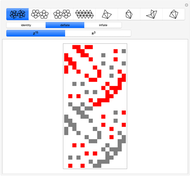
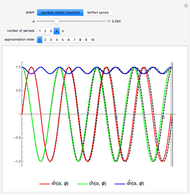
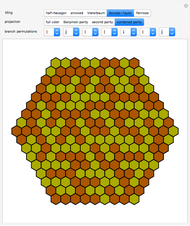
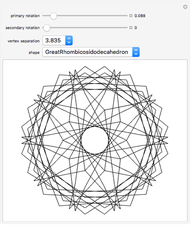
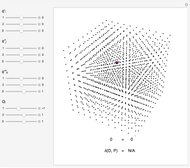
Patterns resulting from the refraction of light through a grating of slits or through a crystal show the phenomena of interference as the sum of path-dependent phases. Thomas Young and Max von Laue first published results on the diffraction of visible light in 1803 and on the diffraction of X-rays in 1912. A simulation can recreate both results using a combination of Huygens' principle and the Fraunhofer or far-field approximation. When the grating is dense on a scale comparable to the wavelength, each infinitesimal region of zero density within a slit emits a spherical wave. When an atomic configuration is not dense on a scale comparable to the wavelength, each point of non-zero density emits a spherical wave. In the limit where the target is far from the grating or atomic configuration, the integral expression describing the diffraction pattern can be rewritten in terms of the Fourier transform. That is, the diffraction pattern is the Fourier transform of some interpretation of the density function. Measurements of diffraction patterns have so accurately characterized the symmetry of crystals that some crystallographers have recently suggested a criterion for a material to be classified as a crystal if its diffraction pattern shows discrete maximums or Bragg peaks. This definition can include crystals with both periodic order and aperiodic order, as these diffraction patterns show.
Contributed by: Brad Klee (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Diffraction in the Fraunhofer limit has long been a solvable problem. The linearity of the Fourier transform makes symbolic solutions easy to compute using just a pencil, a few sheets of paper, and some references. Numeric algorithms designed for use on computers make solutions to the Fraunhofer diffraction problem even easier to compute and display. This Demonstration discretizes some density function onto a  lattice and uses the fast Fourier transform to efficiently compute a diffraction pattern.
lattice and uses the fast Fourier transform to efficiently compute a diffraction pattern.
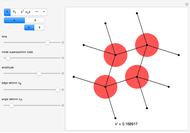
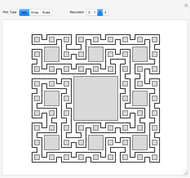
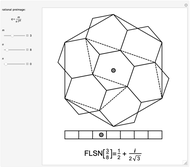
Density functions for slits and periodic crystals are easy to write with conditional logic and the basics of linear algebra. This difficulty of writing aperiodic density functions explains some of the historical bias against the acceptance of aperiodic crystals. Recursive methods of substitution and lattice projections have become more feasible with the advent of computers. Using these methods, aperiodic patterns have become easier to discover and understand. This notebook uses the cut-and-project method to create aperiodic density functions, which list a selection of the vertices from an aperiodic tiling.
References
[1] M. Senechal, Quasicrystals and Geometry, New York: Cambridge University Press, 1995.
[2] B. G. Osgood. "The Fourier Transform and Its Applications." Academic Earth. www.academicearth.org/courses/the-fourier-transform-and-its-applications.
Permanent Citation
"Fraunhofer Diffraction Using a Fast Fourier Transform"
http://demonstrations.wolfram.com/FraunhoferDiffractionUsingAFastFourierTransform/
Wolfram Demonstrations Project
Published: June 18 2012