Free Response in a Second-Order System

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
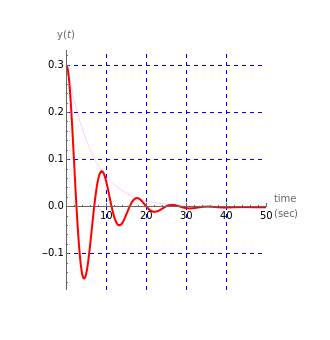
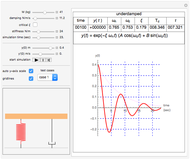
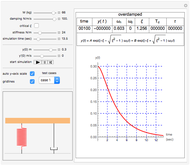
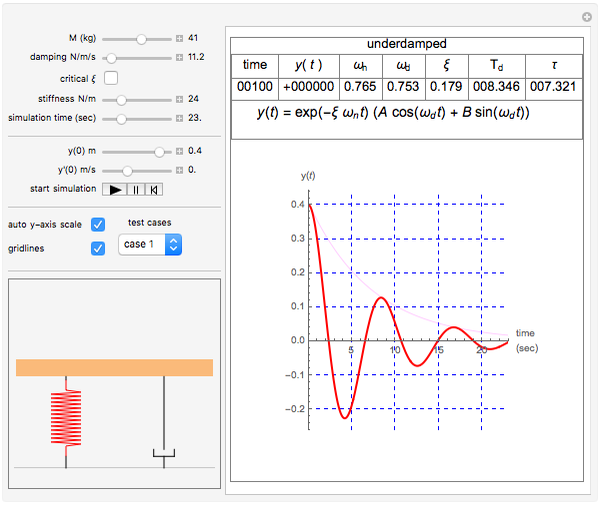
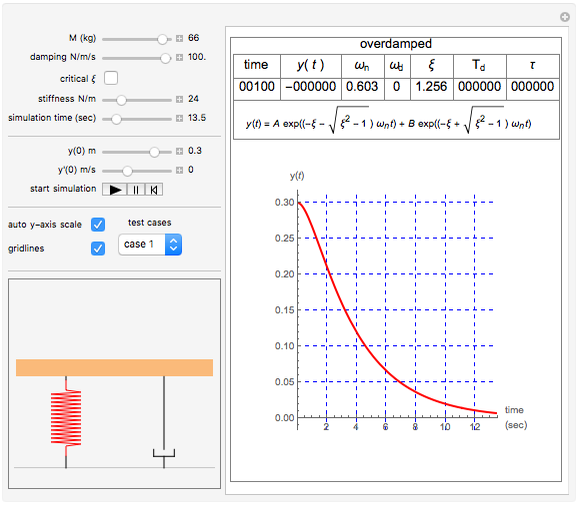
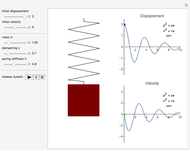
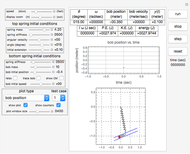
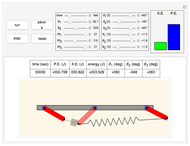
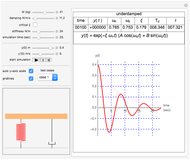
This Demonstration can be used to study the free response of a second-order linear system. You can vary the system parameters (mass, damping, and stiffness) and simulate the response. The analytical solution is displayed at the top of the plot for the cases of underdamping, critically damping, and overdamp. In addition, a standard physical model of mass-spring-damper is run at the same time as the response plot is updated. You can set the initial conditions for initial position and speed using the sliders. Setting the initial conditions to 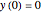 and
and 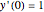 makes the response the same as the impulse response.
makes the response the same as the impulse response.
Contributed by: Nasser M. Abbasi (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The underdamped response of a second-order system is given by 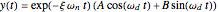 . The critically damped system has the response
. The critically damped system has the response  and the overdamped system has the response
and the overdamped system has the response 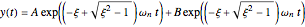 . In all of the above,
. In all of the above, 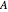 and
and 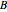 can be found from the initial conditions,
can be found from the initial conditions, 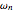 is the natural frequency in
is the natural frequency in 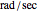 ,
, 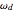 is the damped natural frequency in
is the damped natural frequency in 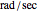 , and
, and  is the damping coefficient.
is the damping coefficient.
For the underdamped case, the damped period of oscillation is given by 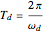 and the time constant is given by
and the time constant is given by 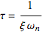 ; both are in seconds. All units displayed are in SI.
; both are in seconds. All units displayed are in SI.
Permanent Citation