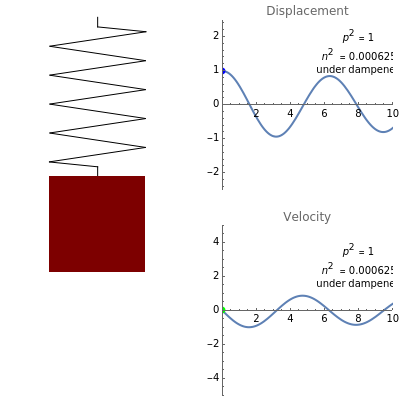
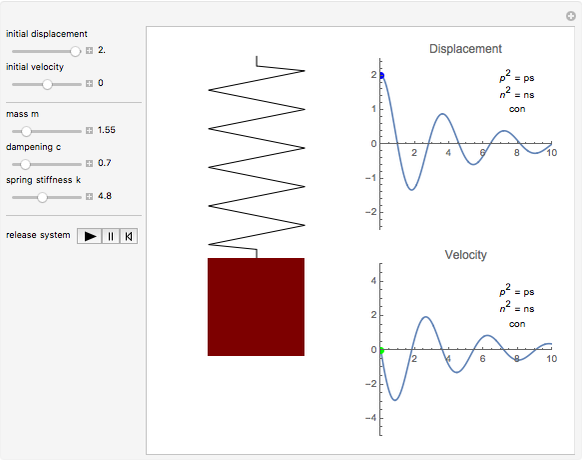
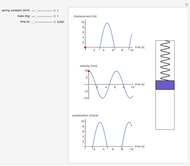
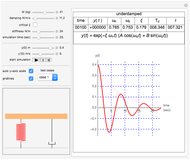
Free Vibrations of a Spring-Mass-Damper System
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The derivation here follows the usual form given in [1], in which 
, 
, and 
are the mass, damping coefficient, and spring stiffness, respectively. The variable in this system is 
. Applying Newton's second law gives the differential equation 
, where 
and 
.
Contributed by: Stephen Wilkerson (Army Research Laboratory and Towson University), Nathan Slegers (University of Alabama Huntsville), and Chris Arney (United States Military Academy, West Point) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference:
[1] S. Timoshenko, D. Young, and W. Weaver Jr., Vibration Problems in Engineering, 4th ed., New York: John Wiley & Sons, 1990.
Permanent Citation
"Free Vibrations of a Spring-Mass-Damper System"
http://demonstrations.wolfram.com/FreeVibrationsOfASpringMassDamperSystem/
Wolfram Demonstrations Project
Published: March 7 2011
Tuned Mass Damper
Nabil Fares
Dynamics of a Double Spring Mass
Stephen Wilkerson (United States Military Academy West Point)
Time Evolution of a Four-Spring Three-Mass System
Michael Trott
Simple Spring Mass Damping
Stephen Wilkerson (Towson University)
Mass on a Spring: Simple Harmonic Oscillator
George Lejnine and Aaron Noble
Free Response in a Second-Order System
Nasser M. Abbasi
Spring-Cart-Pendulum System
Erik Mahieu
Motion of Two Masses Connected by Springs
Sarah Lichtblau
Two Masses with Forcing Functions Oscillating between Three Springs
Stephen Wilkerson
Spring-Launched Ball
Divya Garg and Nimesh Chakravarthi
