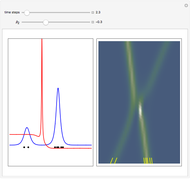
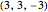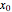From Bohm to Classical Trajectories in a Hydrogen Atom

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
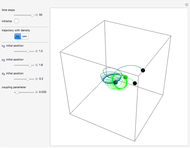
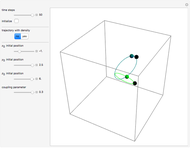
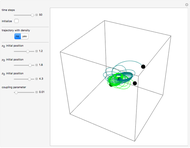
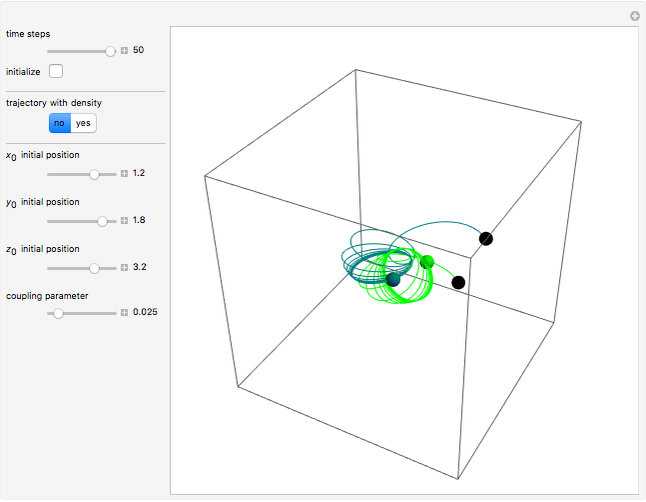
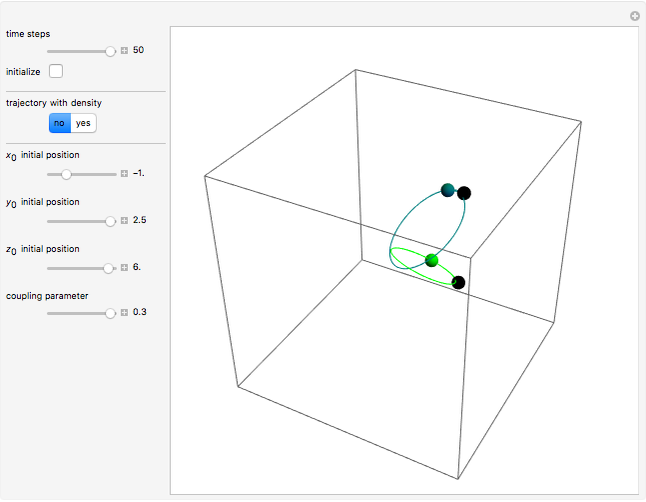
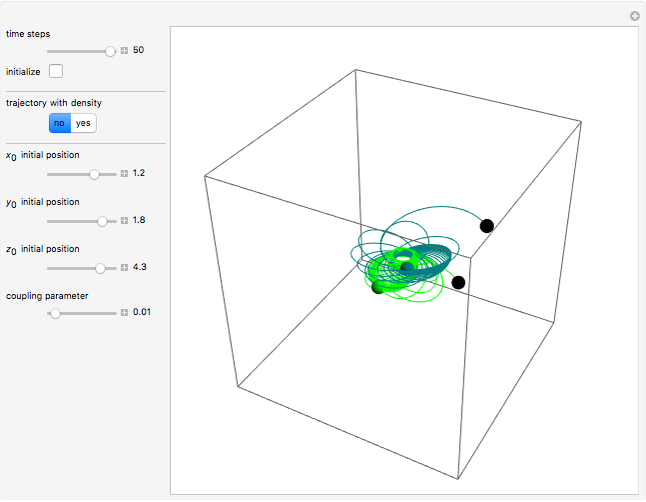
A continuous transition between quantum Bohm trajectories and classical motion is demonstrated. This might be of interest in applications to mesoscopic systems. The hydrogen atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. The Schrödinger equation in spherical polar coordinates for the hydrogen atom is solved by separation of variables. The solutions can exist only when certain constants that arise in the solution are restricted to integer values.
[more]
Contributed by: Partha Ghose and Klaus von Bloh (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
 .
.
For simplicity, set the reduced mass  and
and  equal to 1 (atomic units). This leads to the time-dependent wavefunction with the associated Laguerre polynomials
equal to 1 (atomic units). This leads to the time-dependent wavefunction with the associated Laguerre polynomials 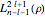 and the spherical harmonics
and the spherical harmonics  :
:
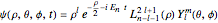 ,
,
with the energy eigenvalue 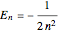 and
and  . The quantum number
. The quantum number  determines the energy,
determines the energy,  is called the orbital quantum number, and the order
is called the orbital quantum number, and the order 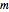 is the magnetic quantum number. For
is the magnetic quantum number. For  , the energy equals
, the energy equals 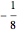 . For
. For  ,
,  ,
,  , in Cartesian coordinates with
, in Cartesian coordinates with 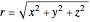 ,
, 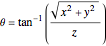 and
and 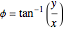 , the wavefunction becomes:
, the wavefunction becomes:
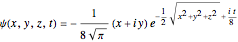 .
.
From the wavefunction for  , the equation for the phase function
, the equation for the phase function 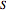 follows:
follows:
 ,
,
and therefore for the components of the velocity:
components of the velocity:
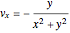 ,
, 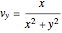 and
and 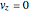 .
.
To see how the Bohmian trajectories smoothly pass over to classical trajectories, the general equation of motion is given by the acceleration term from classical mechanics, which is the second derivative of the position 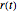 with respect to time
with respect to time  :
:
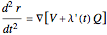 .
.
Here 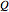 is the quantum potential,
is the quantum potential, 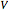 is the Coulomb potential with
is the Coulomb potential with 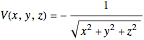 ,
, 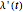 is the environment coupling function, and
is the environment coupling function, and 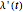 is defined by:
is defined by:
 with
with  and
and 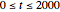 .
.
For our special case, the quantum potential 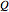 becomes:
becomes:
For more detailed information about the continuous transition between classical and Bohm trajectories, see [1–3] and for an animated example, see [4]. For more detailed information about Bohmian mechanics, see [5].
The results become more accurate if you increase AccuracyGoal, PrecisionGoal and MaxSteps.
References
[1] P. Ghose, "A Continuous Transition between Quantum and Classical Mechanics. I," Foundations of Physics, 32(6), 2002 pp. 871–892. doi:10.1023/A:1016055128428.
[2] P. Ghose and M. K. Samal, "A Continuous Transition between Quantum and Classical Mechanics. II," Foundations of Physics, 32(6), 2002 pp. 893–906. doi:10.1023/A:1016007212498.
[3] P. Ghose and K. von Bloh, "Continuous Transitions between Quantum and Classical Motions." arxiv.org/abs/1608.07963.
[4] P. Ghose and K. von Bloh, Continuous Transitions Between Quantum and Classical Motion for Three Electrons in the Hydrogen Atom [Video]. (Apr 14, 2017) www.youtube.com/watch?v=9pryk-I5Ki0.
[5] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Apr 14, 2017)plato.stanford.edu/entries/qm-bohm.
Permanent Citation