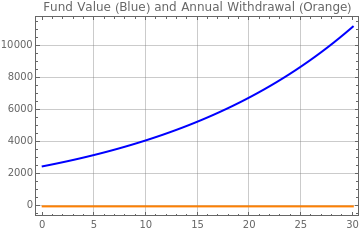
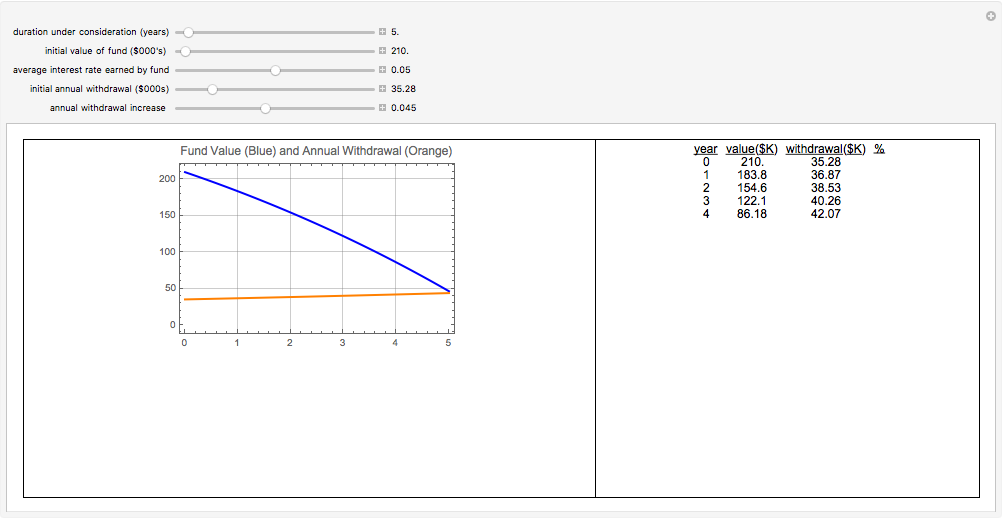
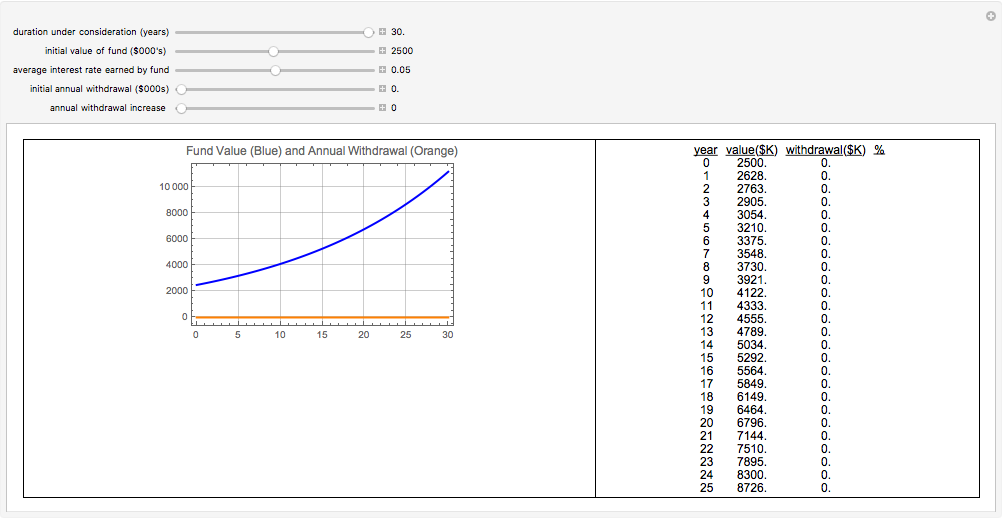
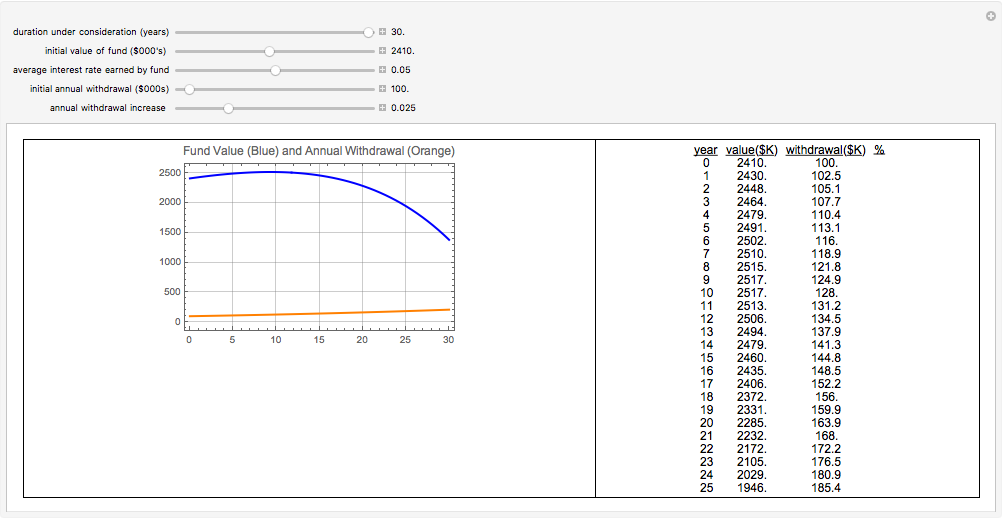
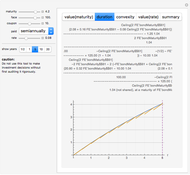
This Demonstration lets you estimate the value of a pool of money (the fund) that increases in value due to an investment return on the fund (at rates between 0 and 10% per year) and decreases in value due to an annual withdrawal. An example would be to estimate how the value of a college fund changes over the four years that tuition and living expenses are withdrawn, while the balance of the fund continues to earn interest. Similarly, the value of a retirement nest egg can be estimated under a situation where the retiree makes annual withdrawals.
A change in the "annual withdrawal increase" applies the selected fractional increase to the value set by the "initial annual withdrawal ($000s)". For example, if the initial annual withdrawal is set at $1000 and the annual withdrawal increase is set at 0.05 (to counter the effects of inflation, say), then the annual withdrawal for the second year will be $1000 x 1.05 = $1050. The annual withdrawal for the third year will be $1050 x 1.05 = $1102.50 and so on.
Here is an equation:
,
where is the annual return as a fractional value, is the annual fractional increase in the withdrawal, and 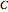is the chosen initial annual withdrawal rate.
This Demonstration solves the above differential equation over a settable range of years, up to 30 years. When the constant annual withdrawal exceeds the investment return, the value of the fund declines over time. In this situation, the "value ($K)" column of the table may turn negative. In this case, the fund has been exhausted and the additional rows and columns of the table are not meaningful.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Browse all topics
