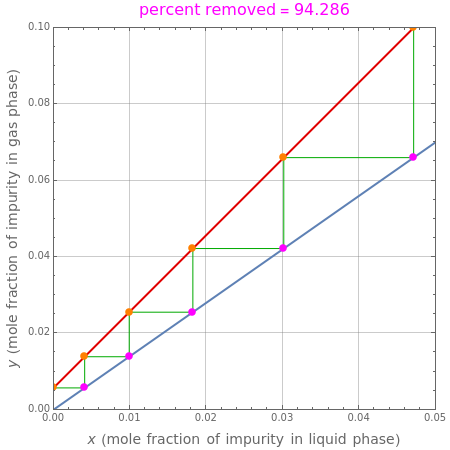
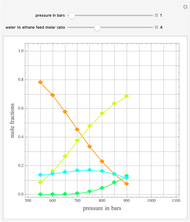
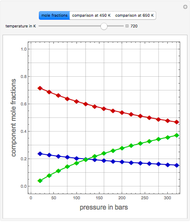
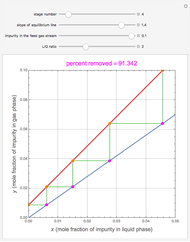
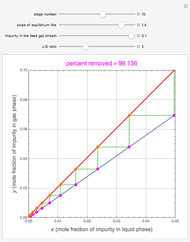
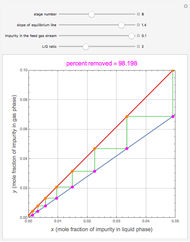
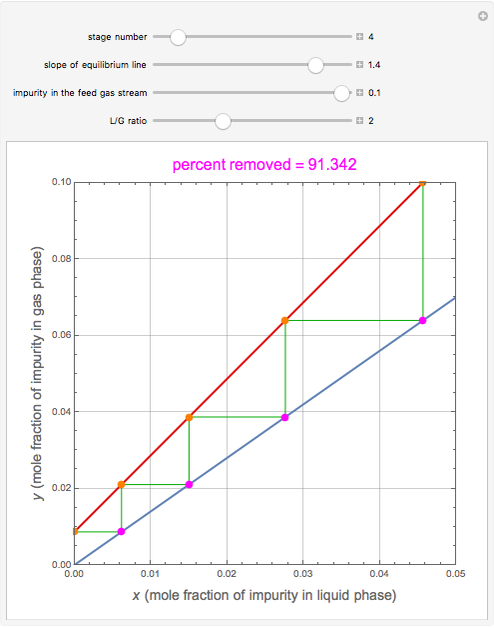
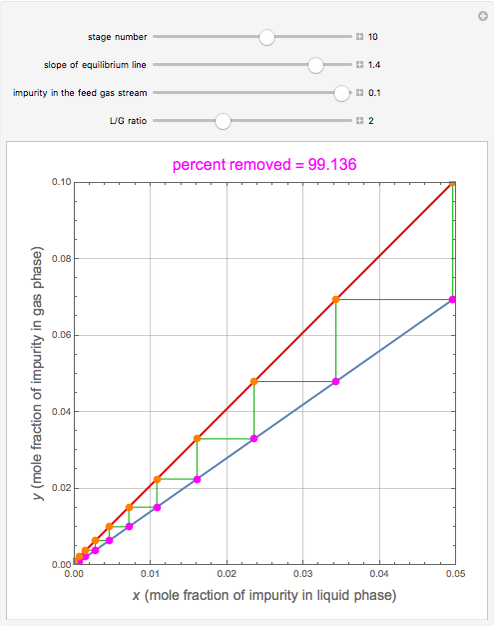
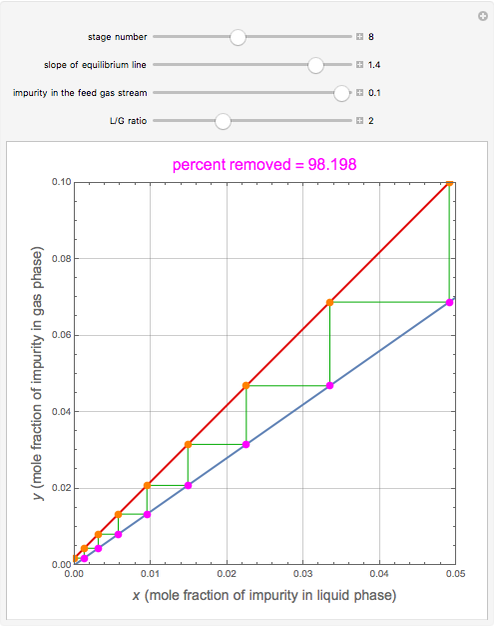
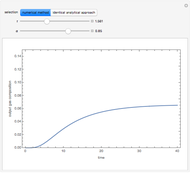
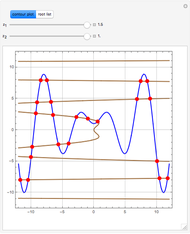
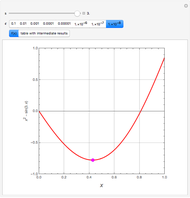
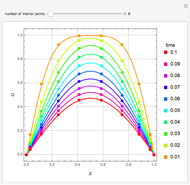
Consider a tray absorption column used to remove an impurity from a gas stream. A pure solvent is used for this absorption operation. The solvent molar flow rate and the gas molar flow rate are considered constant (i.e., the dilute system hypothesis holds). You can set the number of equilibrium stages, the value of the slope of the equilibrium line (), the solvent-to-gas molar flow rate ratio (, and the mole fraction of the impurity in the gas fed to the absorption column. This Demonstration computes the McCabe–Thiele diagram. The horizontal green lines represent the theoretical equilibrum stages in the absorption column. The percent removal of the impurity for the specified conditions is displayed on the plot.