Gaussian Prime Spirals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
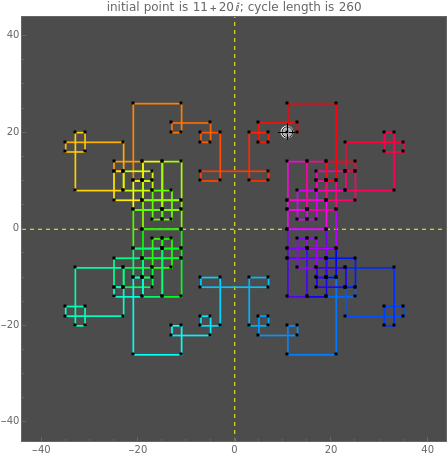
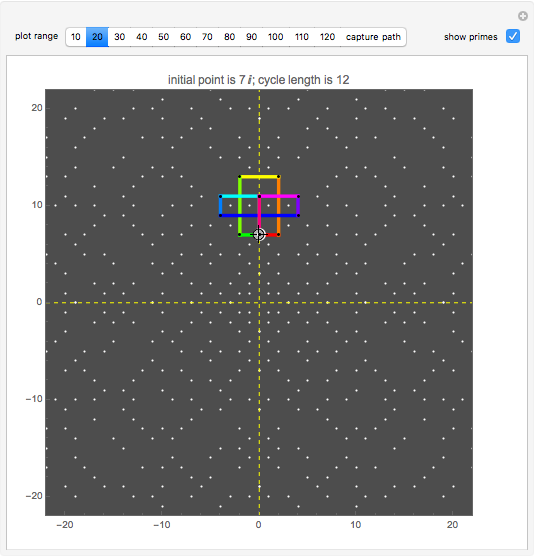
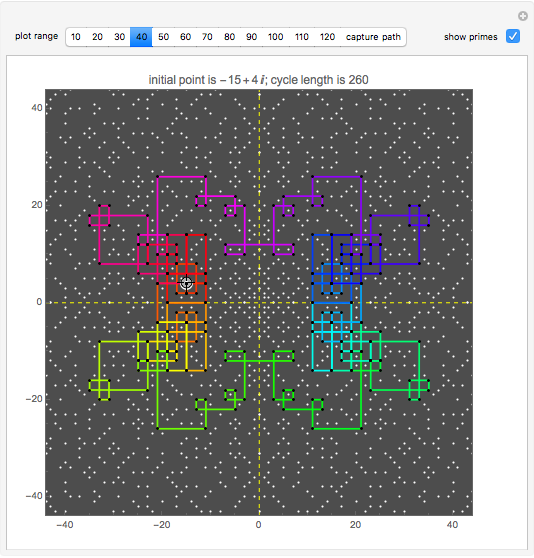
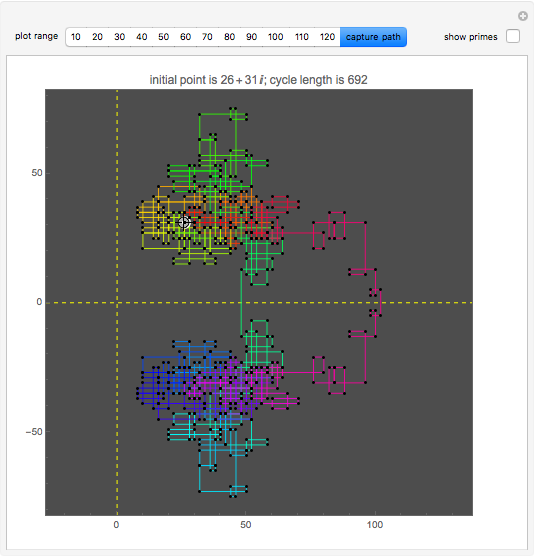
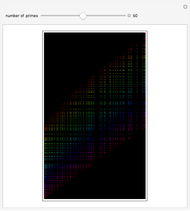
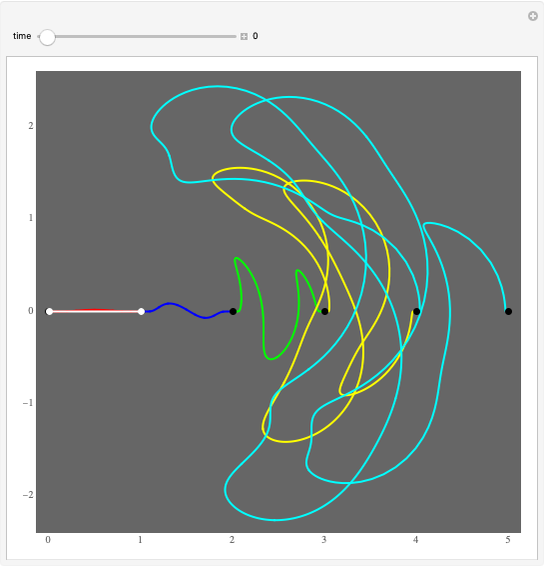
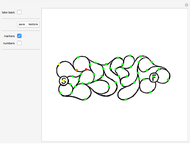
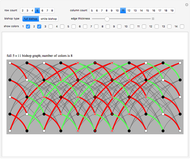
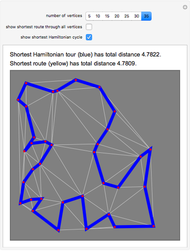
Start a loop with a point having integer coordinates in the complex plane (called a Gaussian integer) and trace a path as follows:
[more]
Contributed by: Joseph O'Rourke and Stan Wagon (April 2012)
(Smith College and Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The problem of whether all initial values lead to closed cycles was first raised in [1]. It is related to the open question: Does every horizontal line contain infinitely many Gaussian primes? This is a consequence of the far-reaching hypothesis H of Schinzel [2]. But even if the horizontal line conjecture is true, it is not clear that starting points always cycle.
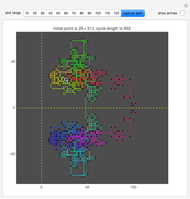
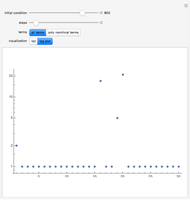
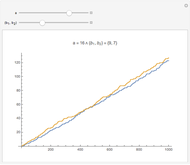
Within the square bounded by ±100, the largest cycle has length 4820 and starts at  . The largest cycle in a search bounded by ±500 starts at
. The largest cycle in a search bounded by ±500 starts at  and has length 316628. The starting value
and has length 316628. The starting value  leads to a walk with 3,900,404 steps.
leads to a walk with 3,900,404 steps.
References
[1] Gaussian prime spirals, MathOverflow question 91423
Permanent Citation