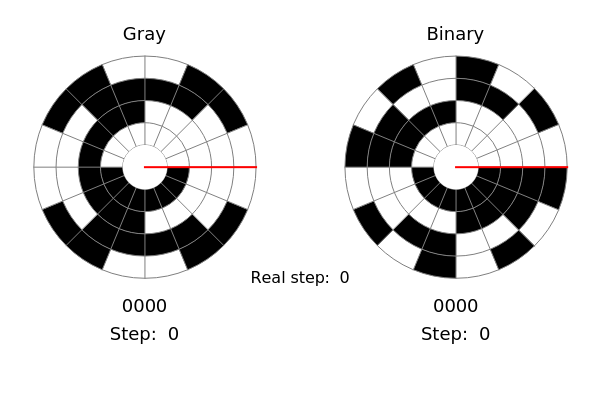
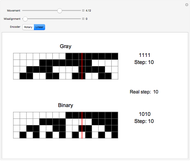
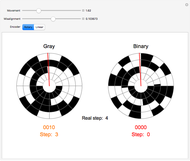
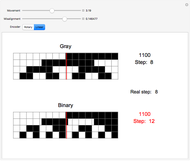
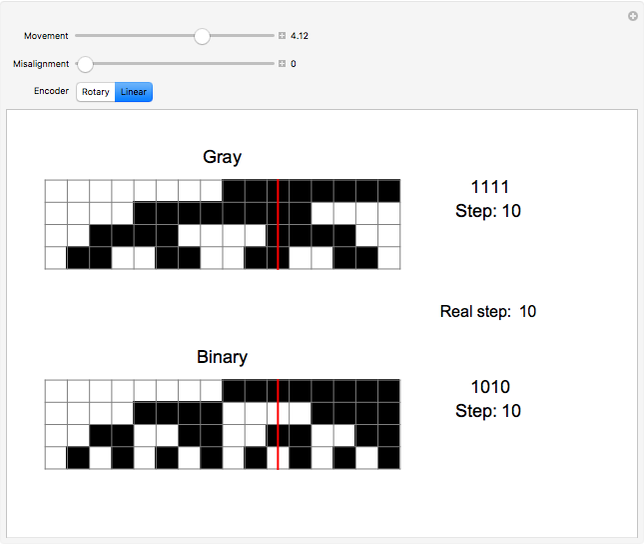
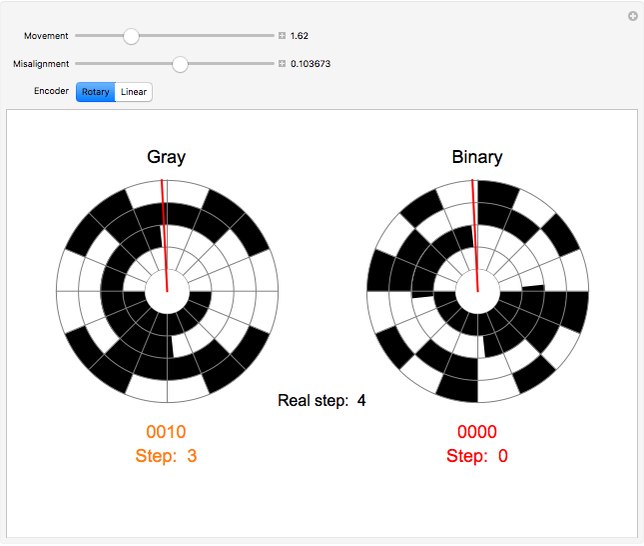
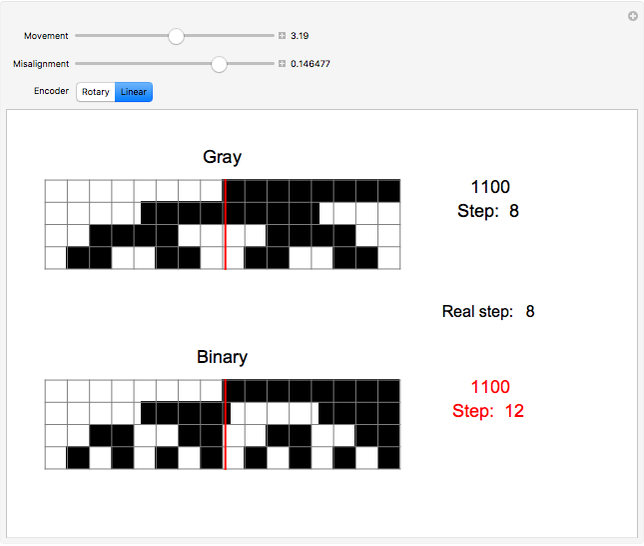
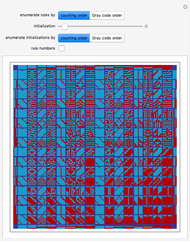
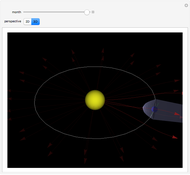
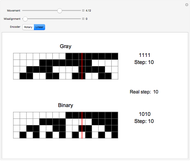
Unlike binary, which follows the sequence 000, 001, 010, 011, 100, and so on, a Gray code is one in which only one bit changes between consecutive steps, such as in the sequence 000, 001, 011, 010, 110, and so on. This has many applications, such as reducing the likelihood of reading an incorrect code from encoders. Two types of encoders are shown in this Demonstration, a rotary encoder used to measure rotation, and a linear encoder used to measure absolute distance. The red sensor reads white contacts as zeros and black contacts as ones, so each position of the sensor yields a unique four-digit code. However, if the positions of the contacts on the encoder are anything less than perfect, the sensor might read an incorrect code. Since a Gray code only varies by one bit for consecutive steps, this will never cause the sensor to read a code that is more than one step away from what it should be, which is shown as the "real step" in the Demonstration. Binary has no limit to how many bits can change between steps, so the transition might cause an illogical sequence, such as from steps three to zero to four. The Demonstration shows this by allowing the contacts for one of the bits to become misaligned. If the sensor reads the correct code, the step is displayed in black; if it is one step away, it is displayed in orange; and if it is more than one step away, it is displayed in red.