Details

According to the prime number theorem (PNT), the number of primes less than or equal to , represented as , is asymptotically . This Demonstration considers how Hawkins' "random primes" fit into the picture.

The standard method for finding primes is called the sieve of Eratosthenes. Start with the prime number 2. Sequentially eliminate all multiples of the most recent prime and take the smallest survivor to be the next prime, then continue the process. For example, the prime 2 would cause every even number to be eliminated. The smallest survivor is 3, so eliminate 6, 9, 12 and so on. The next smallest survivor is 5, and the process continues.

In 1957, Hawkins [1] developed an elegant probabilistic model imitating primes by randomizing the sieve of Eratosthenes. Instead of eliminating in the standard way, starting with 2, let each following number be eliminated with probability 1/2. Continue the process by taking the smallest survivor as the next Hawkins number and eliminate each subsequent integer with probability .

This alternate sieving method based on probabilities produces a different set of numbers than the usual primes. We suppose that the individual primes are not of interest but consider how many there are up to . Unlike the true primes, the count of Hawkins numbers less than or equal to varies depending on the experiment. Now, compute examples and see where they fall relative to .

You can choose between two graphical displays.

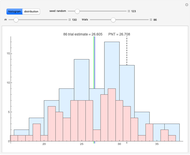
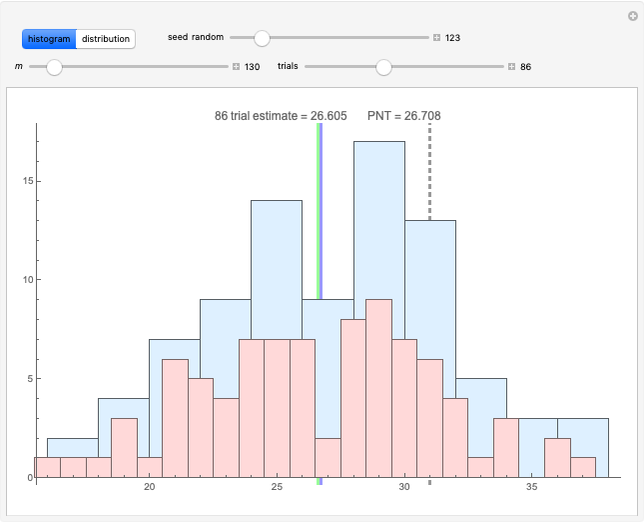
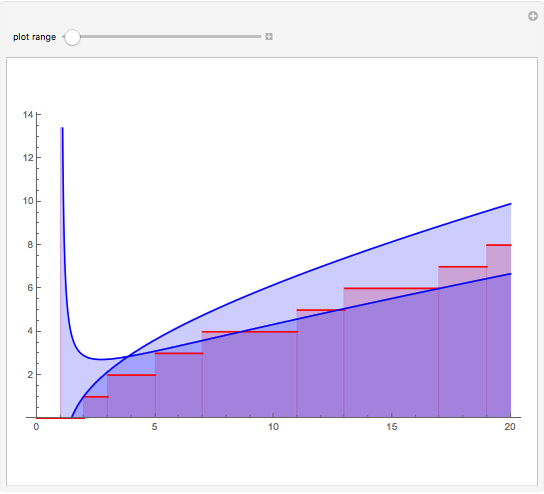
The "histogram" shows two perspectives, wide and unit gradations, for the number of Hawkins numbers found over a given number of trials along with two spikes; the estimate by the PNT is shown in blue and the mean over the trials in green. In general, the estimate is very good even though the distribution is very spread out and asymmetrical.

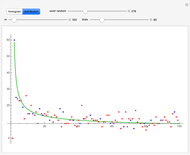
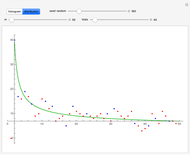
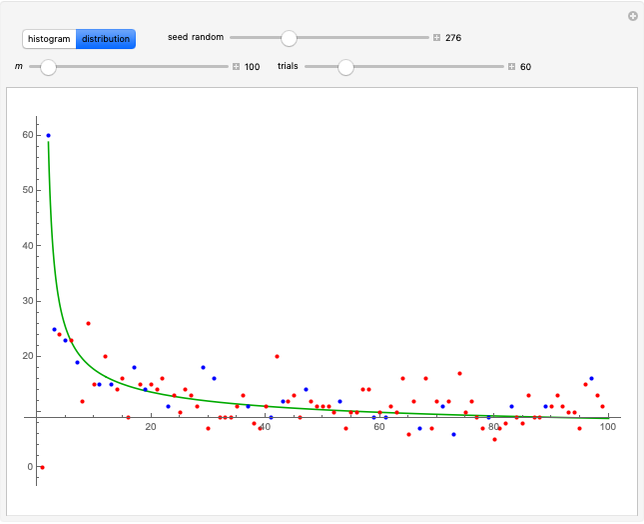
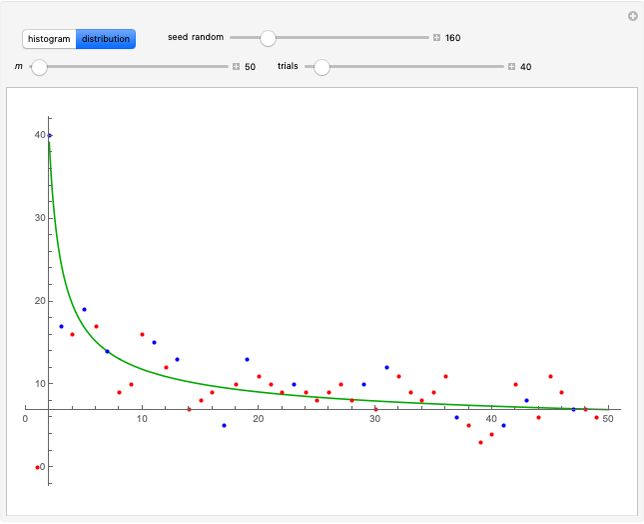
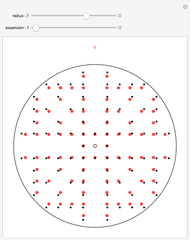
The "distribution" graph displays the density of the frequency of each number between 2 and as a red dot, a Hawkins number over the specified number of trials. Blue dots correspond to true primes.

The green curve was fitted empirically to

and appears to be a good fit for all combinations of and number of trials.

The value of cannot be too large unless the sample size is small because of the extensive computation involved.

Reference

[1] D. Hawkins, "The Random Sieve," Mathematics Magazine, 31(1), 1957 pp. 1–3. doi:10.2307/3029322.