Heisenberg-Type Uncertainty Relation for Qubits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
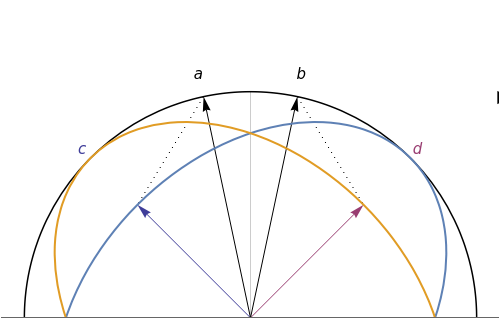
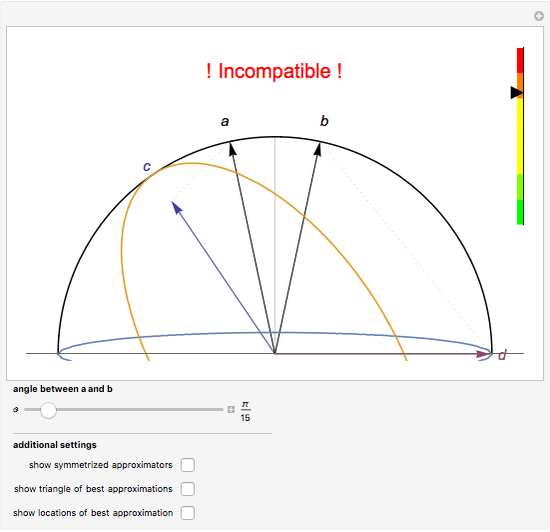
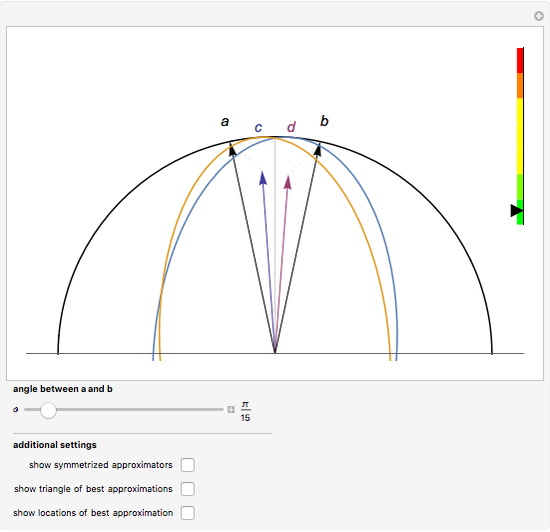
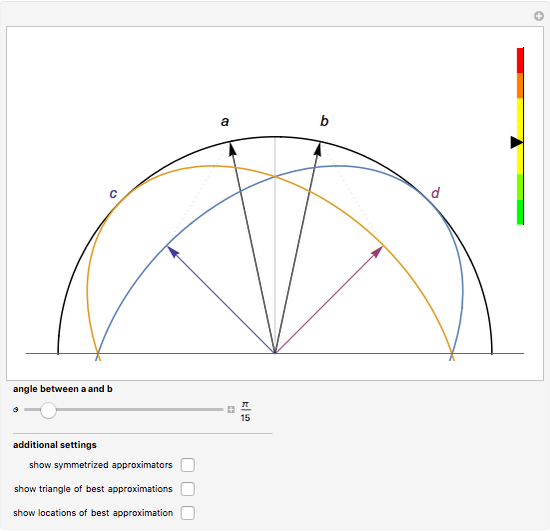
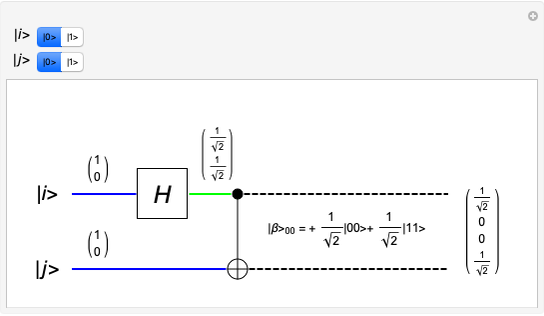
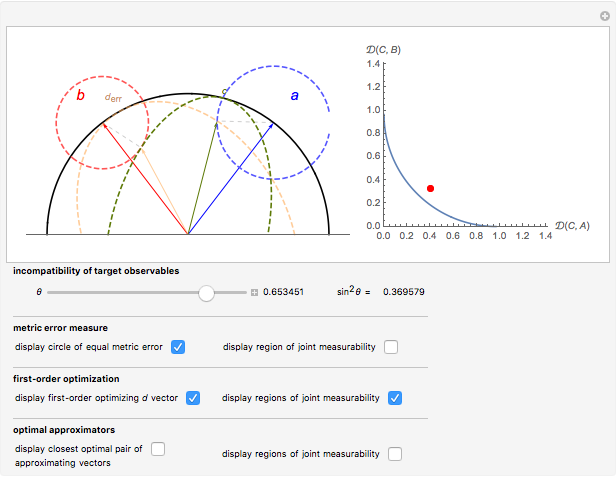
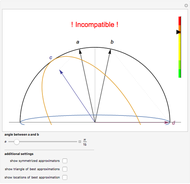
Consider a pair of sharp qubit observables 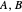 . These observables do not commute and cannot be measured jointly and precisely; they are incompatible. However, allowing for imprecision in the measurement makes it possible to measure approximations
. These observables do not commute and cannot be measured jointly and precisely; they are incompatible. However, allowing for imprecision in the measurement makes it possible to measure approximations 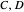 to the noncommuting pair
to the noncommuting pair 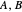 . The approximators
. The approximators 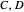 would ideally be chosen so that they give the best possible approximation to
would ideally be chosen so that they give the best possible approximation to 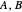 without being incompatible themselves. In this Demonstration, you can explore this choice of
without being incompatible themselves. In this Demonstration, you can explore this choice of 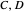 : representing
: representing 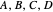 by vectors
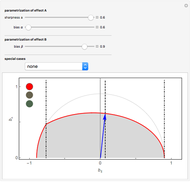
by vectors 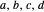 on a vertical slice of the Bloch sphere, the described physical structure translates into geometric constraints. The vectors
on a vertical slice of the Bloch sphere, the described physical structure translates into geometric constraints. The vectors 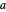 and
and  (both represented by black arrows) are to be approximated by the vectors
(both represented by black arrows) are to be approximated by the vectors  (blue arrow) and
(blue arrow) and  (red arrow), while
(red arrow), while  must be contained in the blue ellipse and
must be contained in the blue ellipse and  must be contained in the red ellipse. You can drag the vectors
must be contained in the red ellipse. You can drag the vectors  . The scale on the right-hand side indicates how well the current choice of
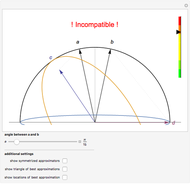
. The scale on the right-hand side indicates how well the current choice of 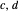 is approximating
is approximating 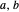 . No choice of approximators
. No choice of approximators  can do better than the minimum of this scale.
can do better than the minimum of this scale.
Contributed by: Johannes Biniok and Paul Busch (August 2014)
Open content licensed under CC BY-NC-SA
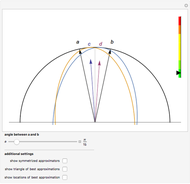
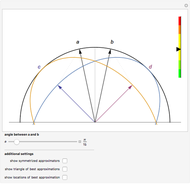
Snapshots
Details
$FailedPermanent Citation