Hidden Variables in Quantum Mechanics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
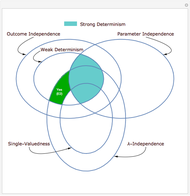
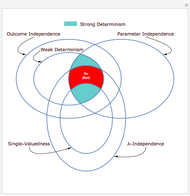
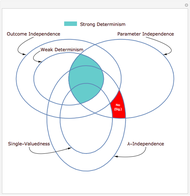
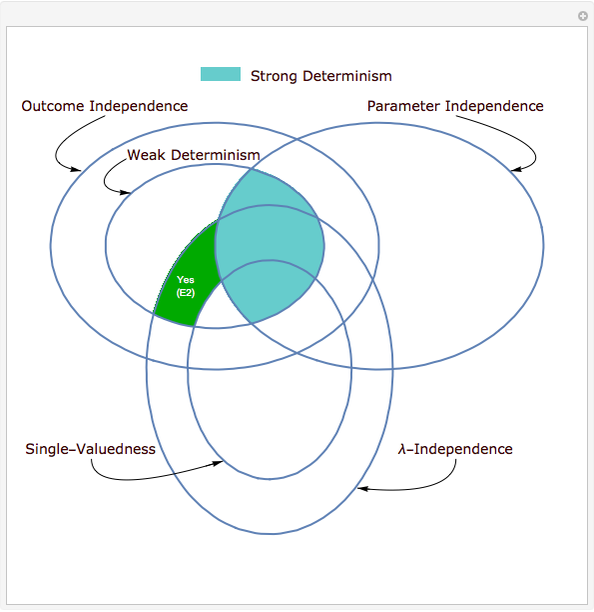
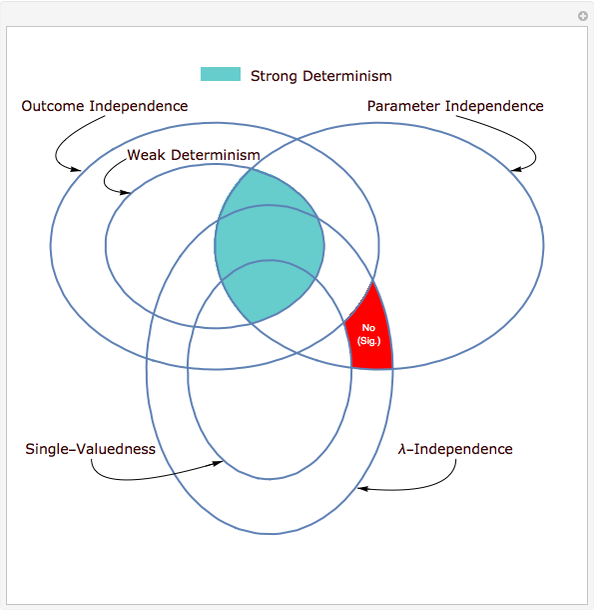
Hidden variables are extra components added to try to banish counterintuitive features of quantum mechanics. There are several different variations of models that describe hidden variables and how they interact with the observable world. This Demonstration covers six possible properties that can be asked of a hidden-variable model. The formal definitions of the six properties are in Details.
[more]
Contributed by: Adam Brandenburger, Ariel Ropek, and Andrei Savochkin (April 2011)
After work by: Adam Brandenburger, H. Jerome Keisler, and Noson Yanofsky
Open content licensed under CC BY-NC-SA
Snapshots
Details
Formally, we consider a space
 .
.
The variables 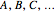 are measurements and the variables
are measurements and the variables 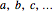 are associated outcomes of measurements. The choice of symbols is meant to represent a situation in which Alice performs a measurement on her particle, Bob performs a measurement on his particle, and so on. We take each of the spaces in
are associated outcomes of measurements. The choice of symbols is meant to represent a situation in which Alice performs a measurement on her particle, Bob performs a measurement on his particle, and so on. We take each of the spaces in  to be finite, and suppose that
to be finite, and suppose that 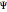 is a finite product.
is a finite product.
Let 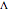 be a finite space on which a hidden variable
be a finite space on which a hidden variable 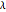 lives. The overall space is then
lives. The overall space is then
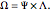
An empirical model is a pair 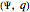 , where
, where  is a probability measure on
is a probability measure on 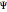 . A hidden-variable model is a pair
. A hidden-variable model is a pair  , where
, where  is a probability measure on
is a probability measure on 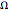 . A hidden-variable model
. A hidden-variable model  realizes an empirical model
realizes an empirical model 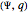 if for all
if for all 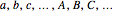 ,
,
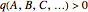 if and only if
if and only if  ,
,
and when both are nonzero,
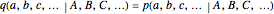 .
.
We can calculate 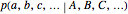 , for
, for  , from the formula
, from the formula
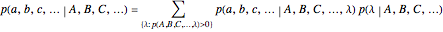 .
.
From this, we see that the idea of equivalence is to reproduce the probability measure  on the space
on the space 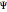 by averaging under a probability measure
by averaging under a probability measure  on an augmented space
on an augmented space 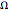 , where
, where 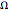 includes a hidden variable. The measure
includes a hidden variable. The measure  is then subject to various conditions.
is then subject to various conditions.
1. A hidden-variable model  satisfies single-valuedness if
satisfies single-valuedness if 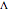 is a singleton.
is a singleton.
2. A hidden-variable model  satisfies
satisfies 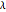 -independence if for all
-independence if for all 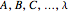 ,
,
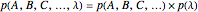 .
.
3. A hidden-variable model  satisfies parameter independence if for all
satisfies parameter independence if for all 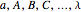 , whenever
, whenever 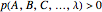 ,
,
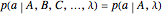 ,
,
and similarly for 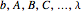 , and so on.
, and so on.
4. A hidden-variable model  satisfies outcome independence if for all
satisfies outcome independence if for all 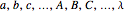 , whenever
, whenever 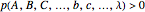 ,
,
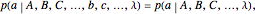
and similarly with  and
and  interchanged, and so on.
interchanged, and so on.
5. A hidden-variable model  satisfies weak determinism if, for every
satisfies weak determinism if, for every 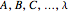 , whenever
, whenever 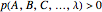 , there is a tuple
, there is a tuple 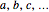 such that
such that 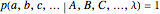 .
.
6. A hidden-variable model  satisfies strong determinism if, for every
satisfies strong determinism if, for every  and
and 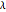 , whenever
, whenever 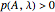 , there is an
, there is an  such that
such that 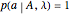 , and similarly for
, and similarly for 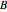 and
and 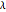 , and so on.
, and so on.
The text that appears in the diagram:
● "E1" refers to Theorem 3.1 in [4].
● "E2" refers to Theorem 3.2 in [4].
● "EPR" refers to the famous Einstein–Podolsky–Rosen argument; see [2].
● "Bell" refers to the famous Bell's theorem; see [1].
● "Sig." refers to any empirical model that is signaling; see [3] for the definition.
References
[1] J. Bell, "On the Einstein–Podolsky–Rosen Paradox," Physics, 1, 1964 pp. 195–200.
[2] A. Einstein, B. Podolsky, and N. Rosen, "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?" Physical Review, 47, 1935 pp. 770–780.
[3] G. C. Ghirardi, A. Rimini, and T. Weber, "A General Argument against Superluminal Transmission through the Quantum-Mechanical Measurement Process," Lettere al Nuovo Cimento, 27, 1980 pp. 293–298.
[4] A. Brandenburger and N. Yanofsky, "A Classification of Hidden-Variable Properties," Journal of Physics A: Mathematical and Theoretical, 41, 2008. doi:10.1088/1751-8113/41/42/425302.
Permanent Citation