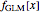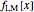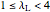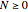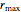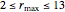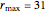Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

High-Precision Newton Algorithm for Generalized Logistic Maps with Unimodality z

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

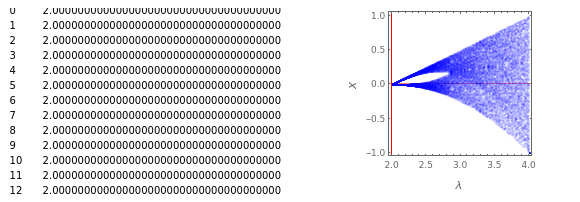
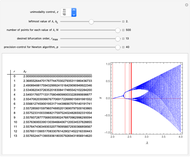
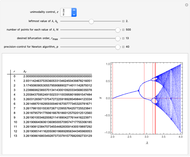
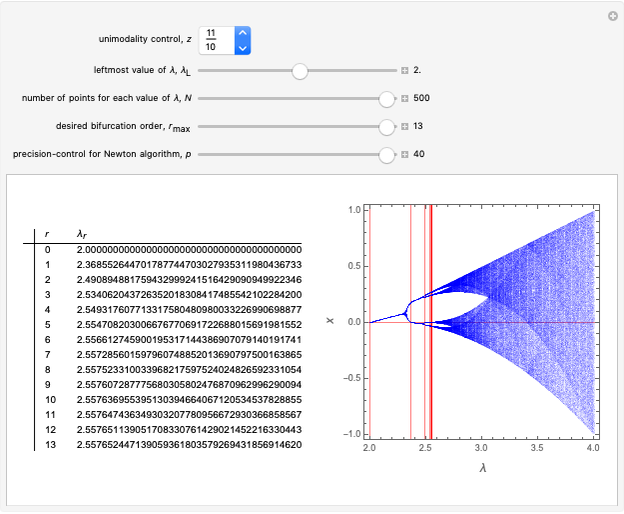
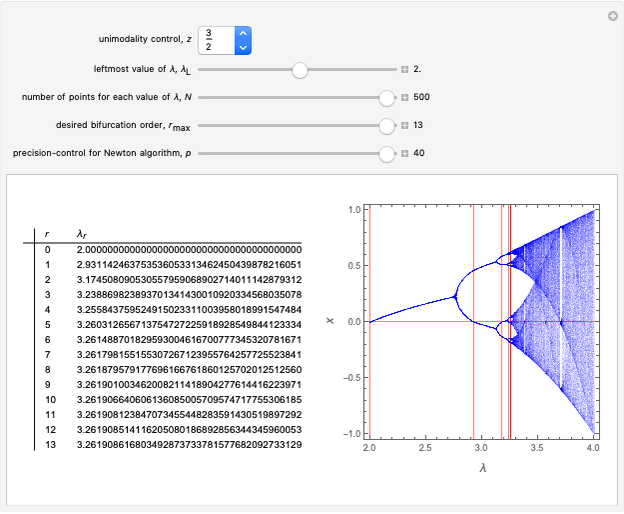
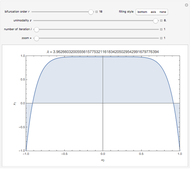
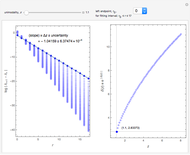
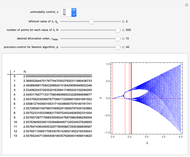
This Demonstration shows a table of superstable parameter values of a period-doubling periodic attractor. The test map is defined as 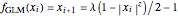, which generalizes the well-known logistic map 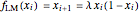. Here is an iteration number, 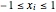, and is the unimodality (or the degree) of the local maximum of 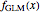. The superstable parameter values are used for the renormalization group analysis of many low-dimensional dynamical systems with chaotic behavior. See the references [1–4].

[more]

The algorithm used is a high-precision Newton algorithm with fixed precision arithmetic. For , superstable parameter values for are exactly the same as those for . In this Demonstration, the required number types and their interval ranges are as follows:

1. is a rational number between 1 and 4.

2. .

3. is an integer, with 0 for the fastest calculation and the poorest visualization; 50 for moderate speed and moderate visualization; and 500 for the slowest speed with good visualization.

(4) is an integer, . You can select higher values manually, but at your own risk. For example, with , the author's computer calculated the super-stable parameter values for for one week! The minimum precision length used for this calculation was 40.

(5) is an integer used in the fixed precision arithmetic. The Newton algorithm for finding superstable parameter values with a low precision may result in wrong answers. High precision is good but it requires a long calculation time. This Demonstration is designed for .

[less]

Contributed by: Ki-Jung Moon (November 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

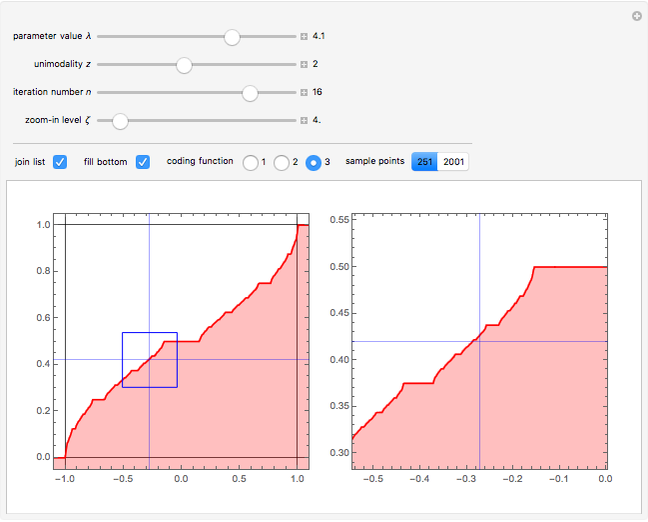
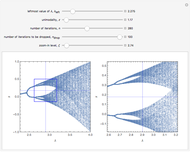
Snapshot 1 for ; snapshot 2 for ; snapshot 3 for 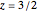; snapshot 4 for 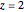; snapshot 5 for . The generalized logistic map is particularly convenient for renormalization group analysis because:

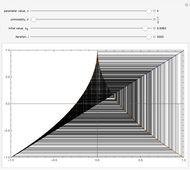
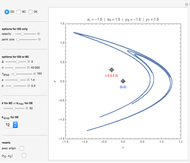
1. The attracting domain (or the basin of attraction) of any periodic/chaotic attractor is strictly confined within 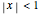for any and .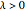

2. All boundary crises occur at for any .

Mitchell J. Feigenbaum's original renormalization group analysis on the classic logistic map can be found in [1] and [2]. More information on the renormalization group analysis can be found in [3] and [4].

References

[1] M. J. Feigenbaum, "Quantitative Universality for a Class of Non-Linear Transformations," Journal of Statistical Physics, 19, 1978 pp. 25–52.

[2] M. J. Feigenbaum, "The Universal Metric Properties of Nonlinear Transformations," Journal of Statistical Physics, 21, 1979 pp. 669–706.

[3] K.-J. Moon, "Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 18, 2008 pp. 023104.

[4] K.-J. Moon, "Erratum: Reducible Expansions and Related Sharp Crossovers in Feigenbaum's Renormalization Field," Chaos: An Interdisciplinary Journal of Nonlinear Science, 20, 2010 pp. 049902.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send