Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

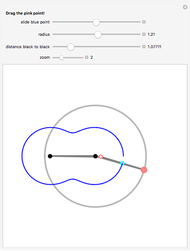
Holditch Curves inside an Ellipse

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

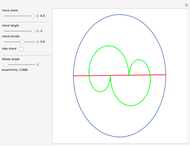
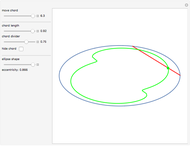
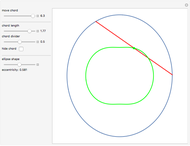
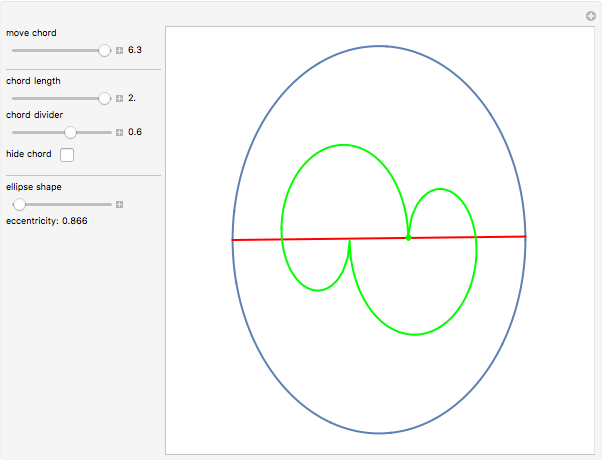
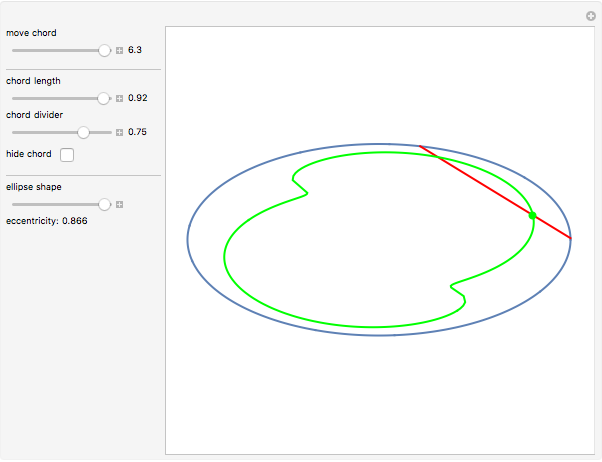
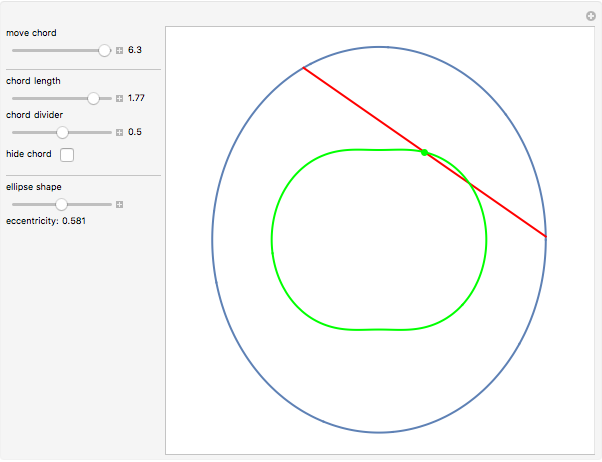
Around 1858, the Reverend Hamnet Holditch studied the curves generated by a point on a chord of fixed length sliding inside another curve.

[more]

This Demonstration is an animation showing the generation of some Holditch curves inside ellipses of different eccentricities. You can see the effect of the chord length and the position of the generating point on the chord.

[less]

Contributed by: Erik Mahieu (April 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The parametric equation of the ellipse is used with the semimajor axis equal to 1 and eccentricity : .

Since there is no simple formula for the chord length along the circumference of an ellipse, you have to continuously solve the equation expressing the intersection of the ellipse and a circle with radius equal to the chord length.

For a description of Holditch's theorem, see [1] and [2].

[1] C. Pickover, The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, New York: Sterling, 2009 pp. 250–251.

[2] J.-P. Truc, Le Théorème de Holditch, Quadrature, 75, 2010 pp. 10–18.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send