How to Design a Building so It Works Like a Termite Mound

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration shows how to optimize the thickness and surface area of thermal mass inside a building, to control the interior temperature and rate of buoyancy ventilation in "free-running" mode. The thermal mass and ventilation are synchronized in a natural feedback loop, similar to the way that termite mounds work. One surprising prediction is that timber can work almost as well as concrete. It is just a matter of tuning the proportions of the building mass correctly.
Contributed by: Salmaan Craig and Remy Fortin (June 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Background
In 2015, King, Ocko and Mahadevan showed how termite mounds harness the diurnal temperature swing for ventilation [1]. In 2018, Craig interviewed the scientists about their findings and wrote about the potential implications for thermally massive architecture [2].
In 2007, Holford and Woods published a mathematical analysis of the coupling of internal thermal mass with buoyancy ventilation [3]. In 2019, Craig used the Holford and Woods model to define optimal proportions for thermally massive buildings [4]. This Demonstration is based on that 2019 article.
Annotated Nomenclature
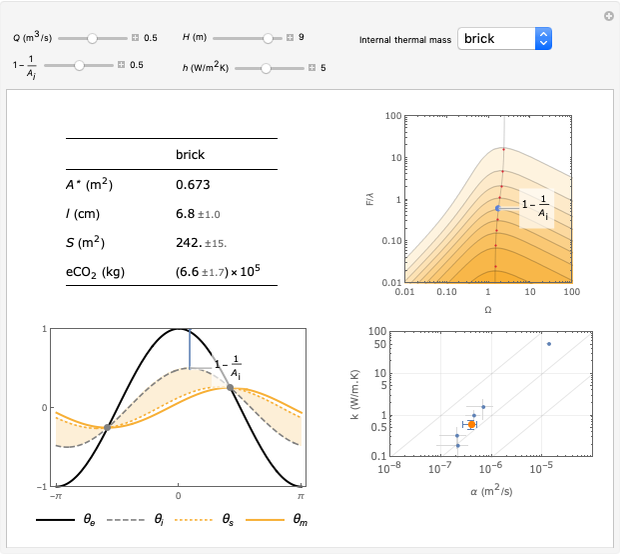
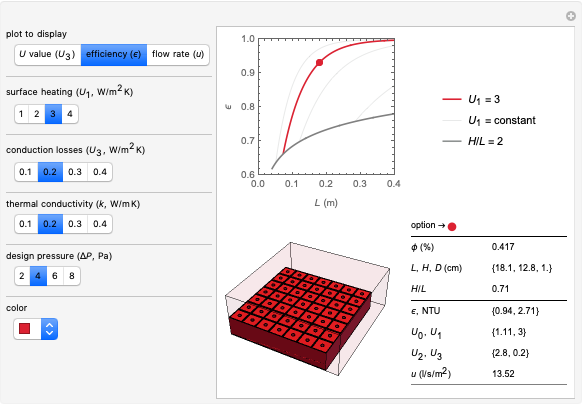
Control panel
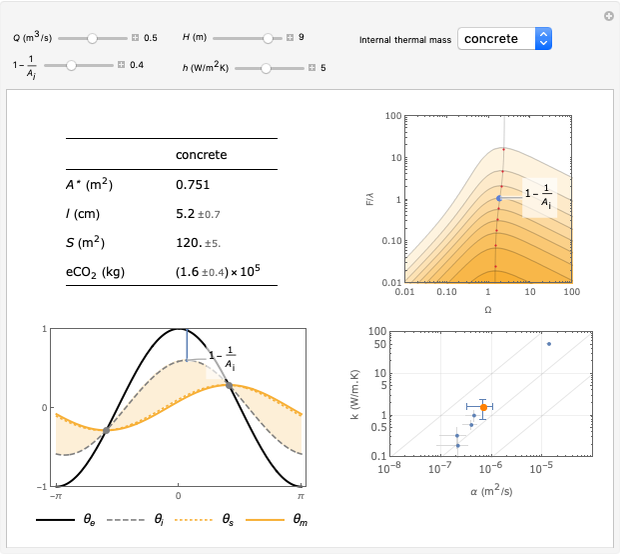
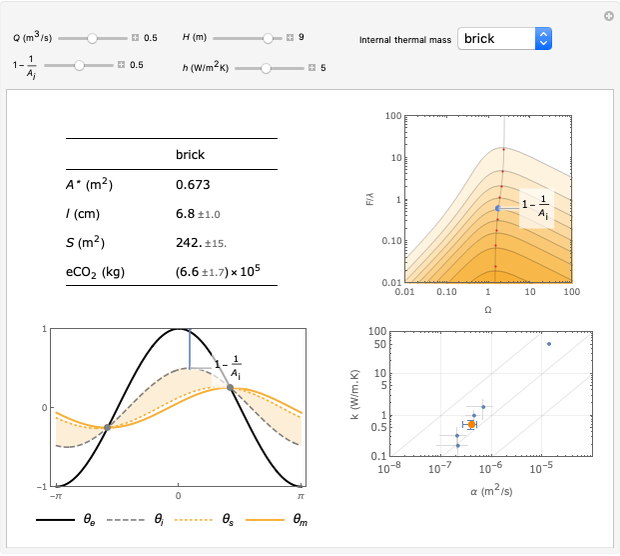
H (m). Building height. Specifically: vertical distance between top and bottom vent.
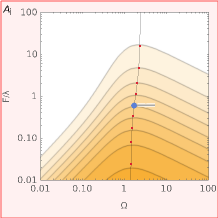
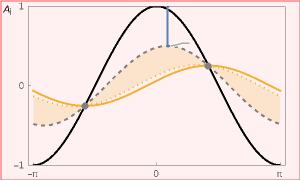
1-1/ (-). Damping coefficient. Defines the maximum "free-running" interior air temperature, relative to the maximum exterior temperature. The chosen damping coefficient is visualized in the bottom-left and top-right graphs.
(-). Damping coefficient. Defines the maximum "free-running" interior air temperature, relative to the maximum exterior temperature. The chosen damping coefficient is visualized in the bottom-left and top-right graphs.
Q ( /s). The average rate of buoyancy ventilation. Choose a value related to occupant needs. For instance, engineering guidelines recommend 10 l/s of fresh air per person in an office environment. Therefore 50 people = 50 * 0.01 = 0.5
/s). The average rate of buoyancy ventilation. Choose a value related to occupant needs. For instance, engineering guidelines recommend 10 l/s of fresh air per person in an office environment. Therefore 50 people = 50 * 0.01 = 0.5  /s. Note that the ventilation is powered by the temperature difference generated by the damping effect of the thermal mass. The ventilation cools the mass during the night (updraft), while the mass cools the ventilation during the day (downdraft). One can increase the input value of Q as a proxy for internal convective loads.
/s. Note that the ventilation is powered by the temperature difference generated by the damping effect of the thermal mass. The ventilation cools the mass during the night (updraft), while the mass cools the ventilation during the day (downdraft). One can increase the input value of Q as a proxy for internal convective loads.
h ( K). Surface heat transfer coefficient, between the thermal mass and the interior. Typical values are
K). Surface heat transfer coefficient, between the thermal mass and the interior. Typical values are  K for surface convection plus
K for surface convection plus  K for surface radiation. One can increase the input value of h as a proxy for internal loads. Note that if all interior surfaces are covered with internal thermal mass at the same temperature, there is no net infrared radiant exchange between those surfaces.
K for surface radiation. One can increase the input value of h as a proxy for internal loads. Note that if all interior surfaces are covered with internal thermal mass at the same temperature, there is no net infrared radiant exchange between those surfaces.
Results table (top left)
A* ( ). Effective open area of vents. The actual area required depends on the geometry of the vents. For instance, say A* = 1. Assume a simple window opening for the top and bottom vents. They are both the same size, and their width and height are much larger than their depth. The friction factor is then
). Effective open area of vents. The actual area required depends on the geometry of the vents. For instance, say A* = 1. Assume a simple window opening for the top and bottom vents. They are both the same size, and their width and height are much larger than their depth. The friction factor is then  0.6 and the required open area of each window is 1/0.6 =1.67
0.6 and the required open area of each window is 1/0.6 =1.67 . See Chapter 2 of [6] for more details.
. See Chapter 2 of [6] for more details.
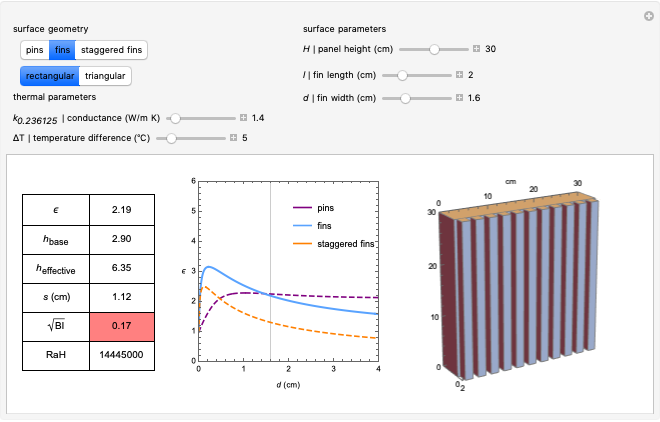
l (cm). Optimal thickness of internal thermal mass. "Thermal mass" is the ability of a building mass to dampen diurnal temperature swings. An "internal" thermal mass is insulated from the exterior thermal environment but exposed to the interior thermal environment. The range (+/-) is due to the uncertainty associated with the thermal properties of the chosen material (see bottom-right graph).
S ( ). Optimal surface area of internal thermal mass. The range (+/-) is due to the uncertainty associated with the thermal properties of the chosen material (see bottom-right graph).
). Optimal surface area of internal thermal mass. The range (+/-) is due to the uncertainty associated with the thermal properties of the chosen material (see bottom-right graph).
e (kg).
(kg).  emissions associated with producing said quantity of internal thermal mass material (i.e. "embodied carbon"). A range of values is given based on the data sheets in Chapter 15 of [5]. The maximum
emissions associated with producing said quantity of internal thermal mass material (i.e. "embodied carbon"). A range of values is given based on the data sheets in Chapter 15 of [5]. The maximum  sequestered by wood is calculated by subtracting 2.8 kg
sequestered by wood is calculated by subtracting 2.8 kg  per kg material (see p. 124, Chapter 6).
per kg material (see p. 124, Chapter 6).
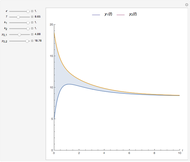
Temperatures versus time (bottom-left graph)
θ (-). Dimensionless temperature. Normalized such that the maximum diurnal temperature is  and the mean diurnal temperature is
and the mean diurnal temperature is  .
.
τ (-). Dimensionless time. Normalized such that  24 hrs.
24 hrs.




Contour map (top-right graph)
Ω (-). Thermal mass parameter. See equation 2.22 in [4].
F/λ (-). Ventilation parameter. See equations 2.24 and 2.25 in [4]. The aim is find the value of  that maximizes
that maximizes  /
/ for a target 1-1/
for a target 1-1/
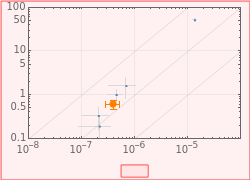
Thermal properties (bottom-right graph)
k (W/m.K). Thermal conductivity. See data sheets, Chapter 15 of [5].
α ( /s). Thermal diffusivity. See data sheets, Chapter 15 of [5]. Note that
/s). Thermal diffusivity. See data sheets, Chapter 15 of [5]. Note that  , where
, where  is the volumetric heat capacity (J/
is the volumetric heat capacity (J/ .K). The diagonal lines in the graph indicate lines of constant
.K). The diagonal lines in the graph indicate lines of constant  .
.
References
[1] H. King, S. Ocko and L. Mahadevan, "Termite Mounds Harness Diurnal Temperature Oscillations for Ventilation," Proceedings of the National Academy of Sciences, 112(37), 2015. doi:10.1073/pnas.1423242112.
[2] S. Craig. "Can Termites Teach Us to Build Environmentally Friendly Communities?" Massive Science. (Apr 1, 2020) massivesci.com/articles/termite-mound-arcology-climate-control.
[3] J.M. Holford and A.W. Woods, "On the Thermal Buffering of Naturally Ventilated Buildings through Internal Thermal Mass," Journal of Fluid Mechanics, 580, 2007. doi:10.1017/S0022112007005320.
[4] S. Craig, "The Optimal Tuning, within Carbon Limits, of Thermal Mass in Naturally Ventilated Buildings," Building and Environment, 165, 2019 106373. doi:10.1016/j.buildenv.2019.106373.
[5] M. F. Ashby, Materials and the Environment: Eco-informed Material Choice, 2nd ed., Boston: Butterworth-Heinemann, 2013.
[6] A. Acred, "Natural Ventilation in Multi-Storey Buildings: A Preliminary Design Approach," Ph.D. thesis, Department of Civil and Environmental Engineering, Imperial College London, 2014. doi:10.25560/34322.
Permanent Citation