Hunter-Nash Method for Liquid-Liquid Extraction (LLE)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
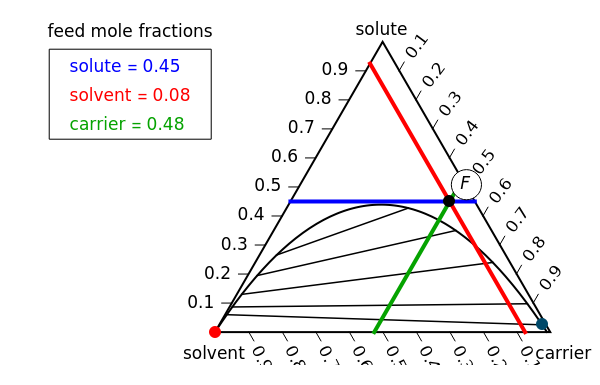
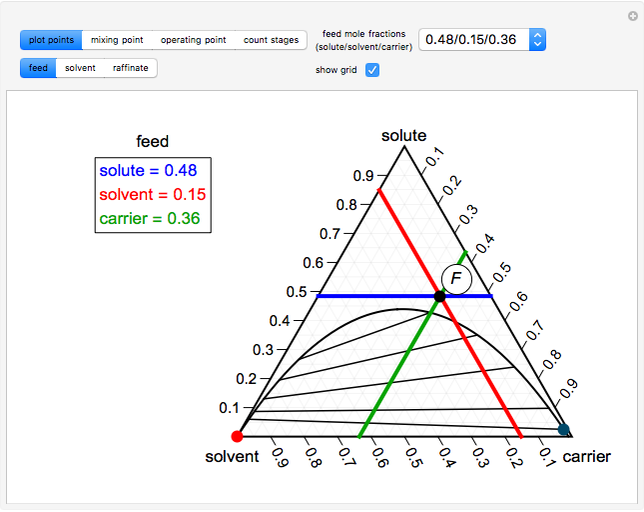
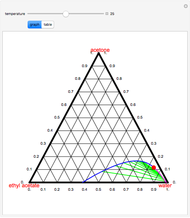
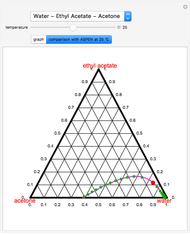
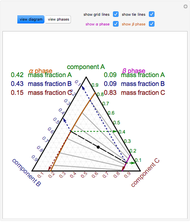
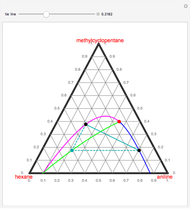
The Hunter–Nash method uses material balances and a ternary phase diagram with phase separation to determine the number of equilibrium stages needed for liquid-liquid extraction (LLE). The system contains a solvent, carrier and solute. Select a feed composition from the drop-down menu. The solvent mass flow rate is given, and the desired raffinate (refined product) composition  is given. Select "plot points" to display the feed (
is given. Select "plot points" to display the feed ( ), solvent (
), solvent (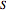 ) or raffinate (
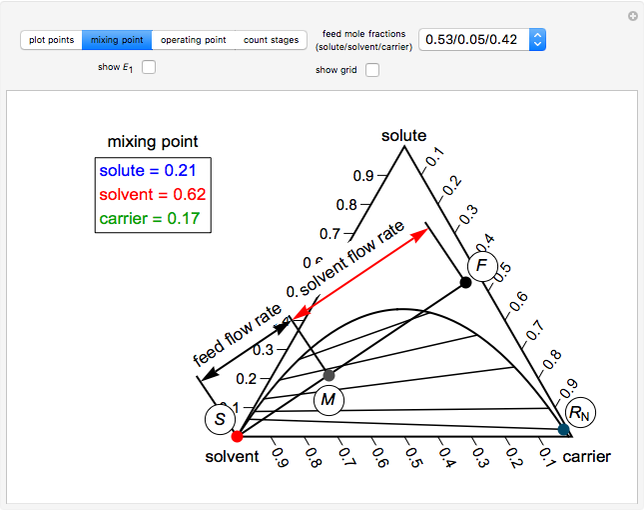
) or raffinate ( ) on the phase diagram. Select "mixing point" to see how the lever rule is used to determine the mixing point (
) on the phase diagram. Select "mixing point" to see how the lever rule is used to determine the mixing point (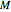 ), and check "show
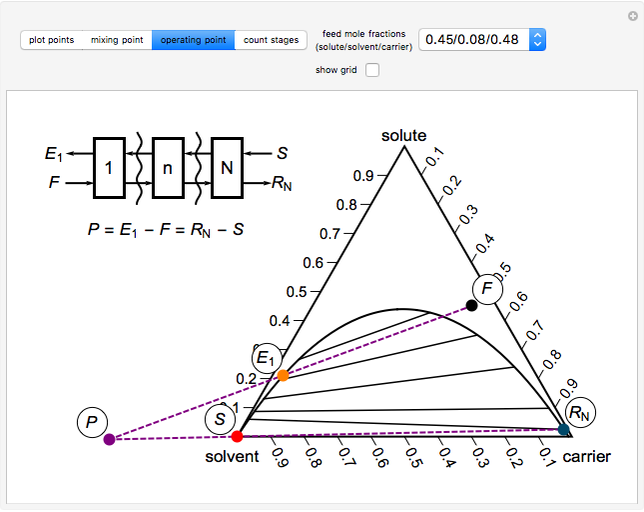
), and check "show  " to see how the extract composition from the first stage is found. Next, select "operating point" to see how the operating point (
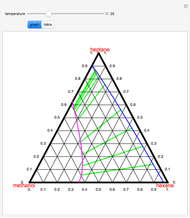
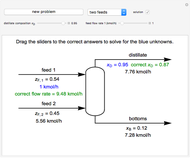
" to see how the extract composition from the first stage is found. Next, select "operating point" to see how the operating point (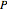 ) is found. This also displays a schematic of the flow system. Finally, select "count stages" and move the "draw tie lines" slider to the right to see how to determine the number of stages and show the raffinate composition leaving each stage. For any of the displays, check "show grid" to display grid lines on the ternary diagram.
) is found. This also displays a schematic of the flow system. Finally, select "count stages" and move the "draw tie lines" slider to the right to see how to determine the number of stages and show the raffinate composition leaving each stage. For any of the displays, check "show grid" to display grid lines on the ternary diagram.
Contributed by: Rachael L. Baumann (October 2015)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
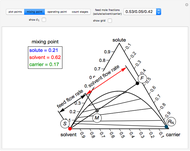
The feed (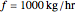 ) flow rate, solvent (
) flow rate, solvent (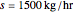 ) flow rate and feed composition (select one of three compositions) are given. The desired raffinate composition is specified, and the extract composition and the number of stages to obtain the desired raffinate composition are determined by mass balances. First, the mixing point composition is calculated and located on the ternary phase diagram. The mixing point corresponds to the composition that would be obtained if the feed and the solvent flows were mixed together:
) flow rate and feed composition (select one of three compositions) are given. The desired raffinate composition is specified, and the extract composition and the number of stages to obtain the desired raffinate composition are determined by mass balances. First, the mixing point composition is calculated and located on the ternary phase diagram. The mixing point corresponds to the composition that would be obtained if the feed and the solvent flows were mixed together:
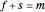 ,
,
solute 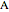 :
:  (because the solvent feed contains no solute),
(because the solvent feed contains no solute),
solvent 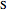 :
:  ,
,
carrier  :
:  .
.
Here 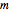 is the combined feed and solvent flow rate (kg/hr) and
is the combined feed and solvent flow rate (kg/hr) and 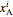 ,
, 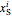 and
and 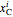 refer to the mass fractions of solute, solvent and carrier in
refer to the mass fractions of solute, solvent and carrier in  (feed
(feed 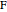 , solvent
, solvent 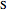 and mixed
and mixed 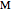 ), which is the stream fed to the cascade.
), which is the stream fed to the cascade.
The mixing point 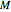 is located on the phase diagram using the lever rule:
is located on the phase diagram using the lever rule:
 ,
,
where  is the line segment from the mixing point
is the line segment from the mixing point 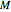 to the feed location
to the feed location 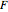 , and
, and  is the line segment from the mixing point
is the line segment from the mixing point 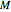 to the solvent location
to the solvent location 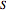 .
.
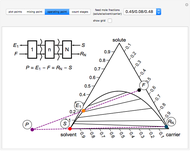
A line drawn from the desired raffinate composition  through the mixing point until it intersects the phase boundary gives the extract composition leaving stage 1,
through the mixing point until it intersects the phase boundary gives the extract composition leaving stage 1,  .
.
The operating point 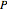 is located at the intersection of a line drawn through points
is located at the intersection of a line drawn through points 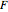 and
and  and a line drawn through
and a line drawn through  and
and 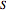 because the overall mass balance for the system is:
because the overall mass balance for the system is:
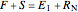 .
.
This equation is rearranged to define the operating point:
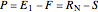 .
.
A tie line from  to the right side of the phase boundary yields the raffinate composition leaving stage 1,
to the right side of the phase boundary yields the raffinate composition leaving stage 1, 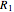 ; this line represents the first equilibrium stage (orange).
; this line represents the first equilibrium stage (orange).
A mass balance on stage 1 (total feed in = total feed out) is:
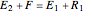 ,
,
which can be written as:
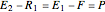 .
.
Thus, the extract composition leaving stage 2, 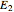 , is found by drawing a straight line from
, is found by drawing a straight line from 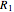 to
to 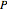 (because
(because 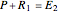 from the previous equation). Where this line intersects the left side of the phase boundary is the composition of
from the previous equation). Where this line intersects the left side of the phase boundary is the composition of 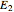 .
.
This procedure is repeated for additional stages until the raffinate composition is nearly equal to the desired value  . The number of orange equilibrium lines drawn is the number of equilibrium stages needed to obtain
. The number of orange equilibrium lines drawn is the number of equilibrium stages needed to obtain  .
.
See [1–4] for screencasts that describe the Hunter–Nash method and present examples.
References
[1] Hunter–Nash Method: Liquid-Liquid Extraction [Video]. (Sep 12, 2016) www.youtube.com/watch?v=e0Yt5RMkyj4.
[2] Hunter–Nash Method: Liquid-Liquid Extraction Example [Video]. (Sep 12, 2016) www.youtube.com/watch?v=FaKIZU3XPR8.
[3] Hunter–Nash Method 1: Mixing and Operating Points [Video]. (Sep 12, 2016) www.youtube.com/watch?v=-yW0jIcH0_E.
[4] Hunter–Nash Method 2: Number of Stages [Video]. (Sep 12, 2016) www.youtube.com/watch?v=JZuavrt8ksQ.
Permanent Citation