Hydrogen-Like Continuum Eigenstates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
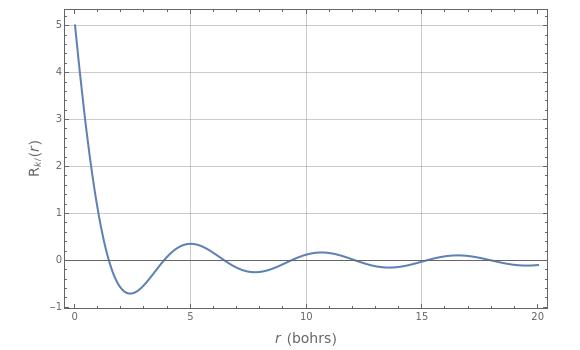
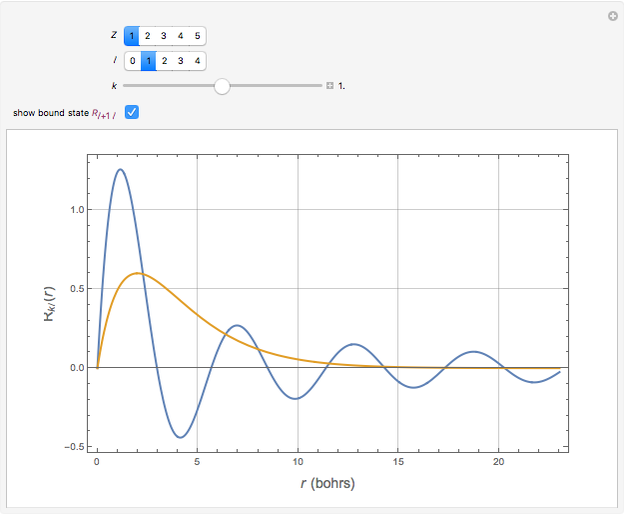
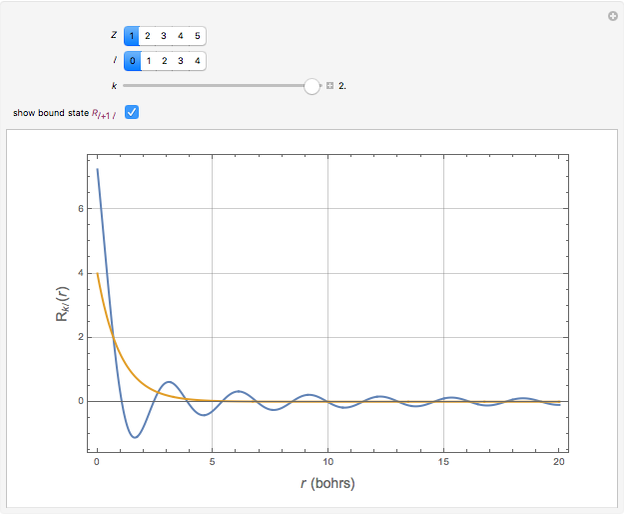
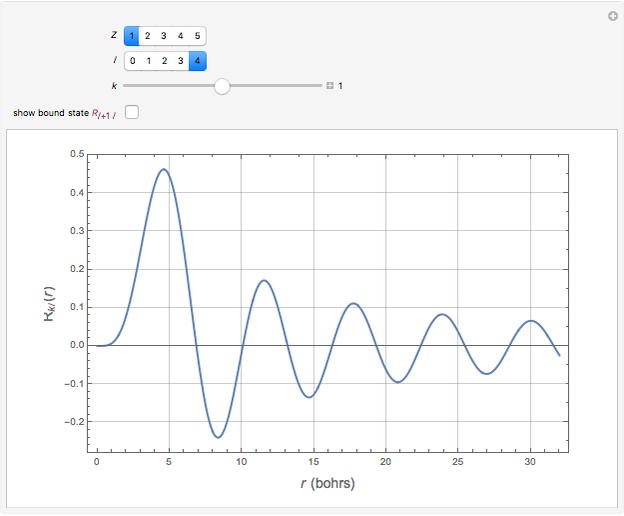
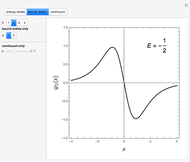
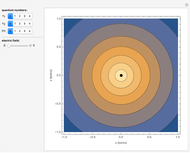
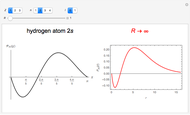
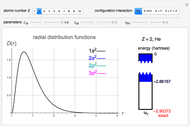
The positive-energy continuum states of a hydrogen-like system are described by the eigenfunctions  with corresponding eigenvalues
with corresponding eigenvalues  , (
, ( ).
).  are the same spherical harmonics that occur for the bound states. In atomic units
are the same spherical harmonics that occur for the bound states. In atomic units  , the radial equation can be written
, the radial equation can be written  . The solutions with the appropriate analytic and boundary conditions have the form
. The solutions with the appropriate analytic and boundary conditions have the form  . These functions are deltafunction-normalized, such that
. These functions are deltafunction-normalized, such that  . They have the same functional forms (apart from normalization constants) as the discrete eigenfunctions under the substitution
. They have the same functional forms (apart from normalization constants) as the discrete eigenfunctions under the substitution  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
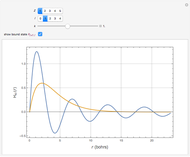
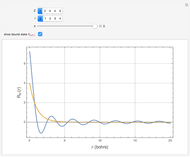
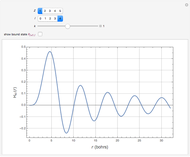
Snapshots
Details
Reference: H. A. Bethe and E. E. Salpeter, Quantum Mechanics of One- and Two-Electron Atoms, New York: Academic Press, 1957, pp. 21–25.
Permanent Citation